![]() ;
;
 ;
;
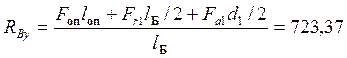 Н.
Н.
![]() ;
;
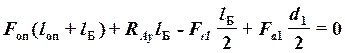 ;
;
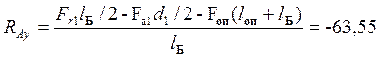 Н.
Проверка:
Н.
Проверка:![]() ;
; ![]() .
.
В соответствии с рис. 3 (см. п. 9.1, с. 16) находим RAx и RBx по формуле:
![]() ;
;
![]() ;
;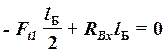 ;
;
![]() Н.
Н.
Проверка: ![]() ;
; ![]() .
.
Тогда в итоге определяем RA и RB по формулам:
![]() Н,
Н,
![]() Н.
Н.
Дано:
Ft2=2230 Н; ![]() Н;
Н;![]() Н;
Н; ![]() м;
м; ![]() м
м
(см. п. 5, табл. 2.1, с. 8 – 9).
В соответствии с рис. 4 (см. п. 9.1, с. 16) находим RCy и RDy по формулам:
![]() ;
;
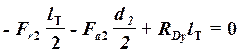 ;
;
. 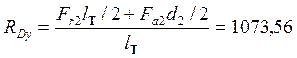 Н
Н
![]() ;
;
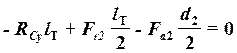 ;
;
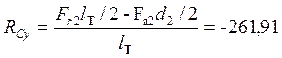 Н.
Н.
Проверка:![]() ;
; ![]() .
.
В соответствии с рис. 4 (см. п. 9.1, с. 16) находим RCx и RDx по формулам:
![]() ;
;
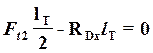 ;
;
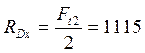 Н.
Н.
![]() ;
;
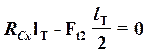 ;
;
 Н.
Н.
Проверка:![]() ;
; ![]() .
.
Тогда в итоге определяем RC и RD по формулам:
![]() Н,
Н,
![]() Н.
Н.
Дано:
Ft1=703,57Н; ![]() Н;
Н;![]() Н;
Н; ![]() Н;
Н; ![]() м;
м;![]() м;
м; ![]() м,
м, ![]() Н,
Н, ![]() Н,
Н, ![]() Н (см. п. 5, табл.
2.1, с. 8 – 9; п. 8.7, с. 15, п. 9.2, с. 17 – 18).
Н (см. п. 5, табл.
2.1, с. 8 – 9; п. 8.7, с. 15, п. 9.2, с. 17 – 18).
Составляем уравнения эпюры изгибающих моментов в рассматриваемых сечениях 1..4 (см. рис. 3, с. 16) и строим её (см. рис. 5, с. 19):
![]() Н∙м;
Н∙м;
![]() Н∙м;
Н∙м; 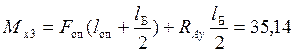 Н∙м;
Н∙м; ![]() Н∙м;
Н∙м;  Н∙м.
Н∙м.
Составляем уравнения эпюры изгибающих моментов в рассматриваемых сечениях 1..4 (см. рис. 3, с. 16) и строим её (см. рис.5, с. 19):
![]() Н∙м;
Н∙м;
![]() Н∙м;
Н∙м; 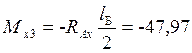 Н∙м;
Н∙м; ![]() Н∙м.
Н∙м.
Дано:
T1 = 19.7 Н∙м (см. п. 3, табл. 1, с. 5).
Строим эпюру крутящего момента, её знак определяется направлением момента от окружной силы Ft1 (см. рис. 5, с. 19).
По рис. 5 определяем суммарные изгибающие моменты в наиболее нагруженных сечениях по формулам:
![]() Н∙м,
Н∙м,
![]() Н∙м.
Н∙м.
Fоп RAy Ft1 RBy
 RA Fa1
RB
RA Fa1
RB
12 4
3
T1 RBx
RAx Fr1
Mв (Н∙м)
![]() Н∙м/мм
Н∙м/мм
Mг (Н∙м)
![]() Н∙м/мм
Н∙м/мм
![]() (Н∙м)
(Н∙м)
![]() Н∙м/мм
Н∙м/мм
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.