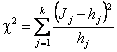Разработка алгоритма основных состояний и системы управления надежности бесстыкового пути. Расчетное прогнозирование полных отказов и показателей долговечности рельсов. Износ крестовин и сроки службы стрелочных переводов. Расчет вероятности безотказной работы элементов стрелочного перевода, страница 6

1. Подсчитывается величина χ² (хи – квадрат) по формуле:

   (3.13)

где J_j и h_j – частоты соответственно статистического и теоретического распределения в j-ом разряде;

j – номер разряда статистического ряда (j=1,2,….k)

частоты теоретического распределения случайной величины могут быть определены по формуле:

   (3.14)

где Р_j - частость теоретического распределения в j-ом разряде;

 - общее число измерений, принятых к исследованию.

2. Определяем число степеней свободы R

R = K – s   (3.15)

где k – число разрядов статистического ряда

s – число наложенных связей или количество числовых характеристик статистического распределения, используемых при расчете координат теоретической кривой распределения.

Для нормального распределения:

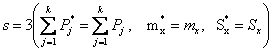   (3.16)

3. Для значения χ² и R по таблице распределения Пирсона (приложение 1) определяется вероятность Р χ² так, что отклонения между теоретическим и статистическим распределением вызваны случайным колебанием измеряемой величины в выборке.

Табличная схема расчета согласованности теоретической и статистической кривых по критерию Пирсона на примере нормального распределения осевых нагрузок приведена в таблице 2.3. (1,2, 6-9). Для данного примера χ² = 5,81, R=12-3=9. Из таблицы приложения 2 определяем Р_χ² = 0,94, что соответствует хорошей сходимости теоретического и статистического распределений. Правило романовского значительно облегчает применение критерия согласия Пирсона для оценки расхождения между теоретическими и статистическими распределениями.

Согласно этому правилу, если:

,

то согласование теоретического и статистического распределений можно считать хорошим. Например, для рассматриваемого примера (таблица 3.3).

,

что свидетельствует о хорошей сходимости теоретического и статистического распределений.

3.4. Описание алгоритма расчета теоретической кривой распределения случайной величины и проверки ее согласия с опытными данными.

Блок – схема  для нормального закона распределения случайной величины приведена на рис. 3.3.

Работа алгоритма начинается с ввода в компьютер числа наблюдений n, минимального числа из статистической совокупности Χmin, значений интервала С разряда, среднего статистического m^*_х, статистического среднего квадратичного отклонения S^*_х, признака критерия согласия z, числа разрядов k статистического ряда (блок 1), а также всех значений частот f_j (блоки 2-5). В блоках 6-14, 18-20 рассчитываются координаты теоретической и статистической кривых распределения случайной величины Х. для этого первоначально переменными j,  присваиваются значения соответственно 1, Хmin (блок 6). Затем производиться построение разрядов статистического ряда путем определения их граничных значений и  (блоки 9,10). Для и  рассчитываются соответственно значения аргументы и  (блоки 7,11) и функции Лапласа Ф() и Ф() – (блоки 8,12).

Координаты теоретической кривой распределения определяются блоком 13. переход к следующему разряду статистического ряда осуществляется с помощью блоков 18-20.

В блоках 6, 14-27 производиться проверка по критериям согласия Пирсона (χ²) и Колмогорова (λ) согласованности теоретической кривой распределения с опытными данными.

Тот или иной критерий согласия выбирается с помощью блоков 15,21. если z=1, то проверка согласия идет по критерию Пирсона (блоки 6-22), иначе при z=0 – по критерию Колмогорова (блоки 56-15, 23-26, 18-21, 27).

При расчетах по критерию Пирсона переменной  χ² вначале присваивается значение ноль (блок 6). Затем в каждом разряде статистического ряда определяется теоретическая частота h_j (блок 16). Значение χ²  накапливается блоком 17, а левая часть неравенства (3.17) рассчитывается блоком 22.

При расчетах по критерию Колмогорова первоначально переменными F_j^* и F_j присваиваются значения ноль. Затем в блоках 22 – 25 для каждого разряда статистического ряда определяются теоретическое и статистическое значение функции распределения случайной величины и разность Rj между ними.

Максимальное значение разности R_max определяется из выражения:

   (3.19)

Первоначально переменной Rmax присваивается значение ноль (блок 6). Затем  эта переменная вычисляется путем последовательной подстановки в правую часть выражения

ее предыдущего значения  и текущего значения разности. Печать производиться в блоке 28.

Рисунок 3.3. Алгоритм расчета теоретической кривой распределения случайной величины и проверки ее согласия с опытными данными

Для определения математического ожидания теоретической кривой распределения воспользуемся формулой:

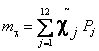  (3.20)

Дисперсию определим по формуле:

     (3.21)

Теоретическое среднее квадратическое отклонение определим по формуле:

  (3.22)

Тогда

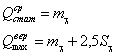
Таким образом, определены все параметры для формул 3.1 – 3.4.

Расчет:

Таблица 3.5

          Итоговые формулы для определения численного значения А имеют вид:

А_Р65 = 4·10^-5β^-1(1+27·10⁴R^-2)=4 ^.10^-5 1,5^-1(1+27 ^. 10^4 . 950^-2)=0,000035

            Формулой для прогнозных расчетов технического (межремонтного) ресурса железнодорожного пути по допускаемому количеству одиночных отказов рельсов [h], шт/км (в среднем по рассматриваемому участку):

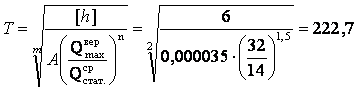
млн. т в год

Ресурс пути в годах между сплошным обновлением верхнего строения пути:

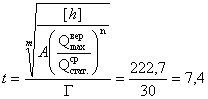 лет

Формула для определения количества одиночных отказов рельсов за последний год перед их сплошной заменой (капитальный ремонт пути):

4.   Износ крестовин и сроки службы стрелочных переводов

4.1. Прогнозирование сроков службы стрелочных переводов