Разработка алгоритма основных состояний и системы управления надежности бесстыкового пути. Расчетное прогнозирование полных отказов и показателей долговечности рельсов. Износ крестовин и сроки службы стрелочных переводов. Расчет вероятности безотказной работы элементов стрелочного перевода, страница 5

Для этого первоначально определяется значение интервала с разрядов и переменными j, x_j^B , f_j присваиваются соответственно значения 1, x_min , 0 (блок 13). Затем рассчитываются значения нижней  x_j^H  и верхней x_j^B  границ разряда (блоки 14, 15). Определение значения частоты в каждом разряде производится из условия   , которое реализовано в блоках 16 – 18.

            Если это условие выполняется, то значение  f_j увеличивается на единицу (блок 19).

В блоках 24 – 30 рассчитывается статистические числовые характеристики: частости   - блок 26, статистического среднего - блок 28, дисперсии D_x^* и S_x^* - блок 30.

Печать результатов производится в блоке 31.

3.3.Выравнивание статистических рядов

Во всяком статистическом распределении неизбежно присутствуют элемент случайности, связанные с тем, что число измерений ограничено, что недостаточно корректно произведены измерения и др. На практике необходимо считаться с тем, что любому статистическому распределению свойственны элементы случайности. Поэтому при обработке статистического материала часто приходиться решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

Подбор закона распределения (принятие гипотезы  о законе распределения), с достаточной точностью описывающего распределение случайной величины, производят, исходя из физической сущности исследуемого процесса или явления. Дополнительными признаками могут служить внешний вид гистограммы или многоугольника распределения и значения числовых характеристик статистического  распределения случайной величины.

Так, для нормального распределения все рассеивания (с точностью до 0,1%) укладываются на участке , для экспоненциального (показательного) распределения , а для пуассоновского распределения .

Для рассматриваемой статистической совокупности гистограмма и многоугольник распределения имеют вид, приведенный на рис. 3.1. по их внешнему виду можно предположить, что осевые нагрузки можно описать нормальным законом распределения.

Для проверки гипотезы о законе распределения измеряемой случайной величины производят расчет координат теоретической кривой распределения и проверку ее согласия со статистическим распределением.

Координаты теоретической кривой распределения рассчитываются для граничных значений разрядов статистического ряда по его числовым характеристикам путем нахождения вероятности Р попадания измеряемой случайной величины в определенный интервал.

Рисунок 3.2. Алгоритм построения статистического ряда и определения его числовых характеристик

Для нормального закона распределения измеряемой случайной величины Х вероятность попадания ее в j-й интервал определяется по формуле:

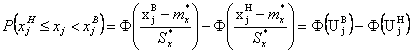   (3.10)

где x_j^H - x_j^B – соответственно нижняя и верхняя границы значений случайной величины Х в j-ом разряде статистического ряда;

 - стандартная функция Лапласа

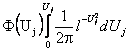,   (3.11)

значения которой табулированы в зависимости от аргумента U_j,

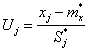,   (3.12)

где j – номер разряда статистического ряда (j=1,2…k).

например, для первого разряда статистического распределения (таблица 3.1.), описываемого нормальным законом (m_x^*=20,48 тс, S_x^* = 5,14 тс) вероятность нахождения осевой нагрузки грузового поезда Х в интервале 8 – 10,8 будет равна:

.

Расчет координат теоретической кривой распределения случайной величины удобно производить с помощью табличной схемы. Так, например, в таблице 3.3 (графы 1 – 6) приведена схема расчета координат теоретической кривой нормального закона, описывающего распределение осевых нагрузок (таблица 3.1).

По рассчитанным значениям координат Р_j строится теоретическая кривая распределения случайной величины (см. рис. 3.1).

Между теоретической и статистической кривыми распределения неизбежны расхождения. Они могут вызываться случайными отклонениями и колебаниями измеряемой величины или другими факторами, которые не были учтены в теоретическом распределении. Эти отклонения могут быть также вызваны неудачным подбором теоретической кривой распределения.

Вопрос согласованности теоретического  и статистического распределения решается с помощью так называемых «критериев согласия.

Наиболее распространенным в практике измерений являются критерии Пирсона и Колмогорова. При проверке согласованности теоретического и статистического распределения по критерию Пирсона выполняются следующие операции.

Таблица 3.3

j	xjH - xjB	xjГР			Рj	hj	fj		Рj*	Fj*	Fj	R=( Fj*- Fj)
1	2	3	4	5	6	7	8	9	10	11	12	13
		8	-2,43	-0,4925				0
1	8-10,7	10,7	-1,91	-0,4719	0,02	2	2	0,08	0,025	0,08	0,02	0,06
2	10,7-12,7	12,7	-1,52	-0,4357	0,04	3	3	0,00	0,038	0,08	0,06	0,02
3	12,7-14,7	14,7	-1,13	-0,3708	0,06	5	6	0,13	0,075	0,20	0,12	0,08
4	14,7-16,7	16,7	-0,74	-0,2704	0,10	8	8	0,00	0,100	0,20	0,22	-0,02
5	16,7-18,7	18,7	-0,35	-0,1368	0,13	11	11	0,01	0,138	0,21	0,36	-0,14
6	18,7-20,7	20,7	0,04	0,016	0,15	12	13	0,05	0,163	0,26	0,51	-0,25
7	20,7-22,7	22,7	0,43	0,1664	0,15	12	10	0,34	0,125	0,61	0,66	-0,05
8	22,7-24,7	24,7	0,82	0,2939	0,13	10	9	0,14	0,113	0,75	0,79	-0,04
9	24,7-26,7	26,7	1,21	0,3869	0,09	7	8	0,04	0,100	0,79	0,88	-0,09
10	26,7-28,7	28,7	1,60	0,4452	0,06	5	5	0,02	0,063	0,81	0,94	-0,12
11	28,7-30,7	30,7	1,99	0,4767	0,03	3	3	0,09	0,038	0,91	0,97	-0,06
12	30,7-32	32	2,24	0,4875	0,01	1	2	1,49	0,025	2,40	0,98	1,42
	Итого:				0,98	78	80	2,40	1,00