Разработка алгоритма основных состояний и системы управления надежности бесстыкового пути. Расчетное прогнозирование полных отказов и показателей долговечности рельсов. Износ крестовин и сроки службы стрелочных переводов. Расчет вероятности безотказной работы элементов стрелочного перевода, страница 3

 - максимально вероятная нагрузка на рельс на рассматриваемом участке

[h] = 6 шт/км.

Заменив в уравнении (1) текущее значение h на [h] допускаемое, решим уравнение относительно Т:

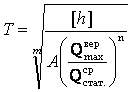  (2)

Это выражение называется формулой для прогнозных расчетов технического (межремонтного) ресурса железнодорожного пути по допускаемому количеству одиночных отказов рельсов [h], шт/км (в среднем по рассматриваемому участку).

 ,

где t – время в годах.

Ресурс пути в годах между сплошным обновлением верхнего строения пути.

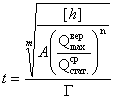    (3)

Формула для определения количества одиночных отказов рельсов за последний год перед их сплошной заменой (капитальный ремонт пути)

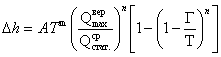   (4).

На основе имеющихся данных для современных стандартных рельсов рекомендуется качестве расчетного значения применить параметр m=2.

Значения параметра А зависит от типа рельсов, их качества (вида термической обработки и раскисления), а также от плана линии.

Для типовых (серийных) незакаленных рельсов Р50, Р65, Р75 в прямых участках пути применительно к среднесетевой совокупности осевых нагрузок (Q_СТ = 14,0 тс/ось) и установленному для таких условий ресурсу, млн.т. брутто (соответственно [Т_Р50] = 350, [Т_Р65] = 500, [Т_Р75] = 600, значения параметра А будут равны:

А_Р50 = 4·10^-5, А_Р65 = 2·10^-5, А_Р75 = 1,389·10^-5.

Эти значения параметра А, как наиболее проверенные опытом эксплуатации и признанные, необходимо использовать в расчетах пути на надежность как базовые.

Для термоупрочненных стандартных рельсов и раскисленных по новой технологии современными лигатурами вводится коэффициент β, равный соответственно 1,5 и 1,25, а при реализации и термоупрочнении и новой технологии раскисления – 1,75.

Для кривых вводиться коэффициент

α=1+27·10⁴R^-2,

где R – радиус кривой, м.

Итоговые формулы для определения численного значения А имеют вид:

А_Р50 = 4·10^-5β^-1(1+27·10⁴R^-2)   (5)

А_Р65 = 2·10^-5β^-1(1+27·10⁴R^-2)   (6)

А_Р75 = 1,389·10^-5β^-1(1+27·10⁴R^-2)   (7)

Численные значения показателя степени n в уравнении (1) при аппроксимации частных экспериментальных выборок может изменяться от 0,9 до 2,1. В качестве расчетной величины предлагается принять наиболее вероятное его значение n = 1,5.

Функция N(Т) = АТ^m снизу ограничена Т=0. Сверху она не имеет ограничения до двойного нормативного ресурса. Функция N(Q) = 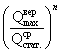снизу ограничена значением Q = 0, а сверху максимальным значением Q, соответствующем началу пластическим деформациям изгиба.

3.1.  Расчет среднестатистической и максимально вероятной осевых нагрузок  ,

 Результаты измерений осевых нагрузок зафиксированы в задании на курсовой проект в порядке их поступления. Так, например, получены следующие ре5зультаты измерений осевых нагрузок от грузового подвижного состава, тс/ось:

8	10,7	14,7	13,7	15,7	13,7	16,7	19,7	18,7	19,7	17,7	20,7	18,7	18,7	22,7
9,7	10,7	13,7	13,7	12,7	14,7	30,7	29,7	28,7	27,7	27,7	27,7	24,7	24,7	23,7
21,7	11,7	15,7	14,7	32	26,7	26,7	27,7	24,7	22,7	23,7	21,7	16,7	16,7	24,7
25,7	22,7	23,7	21,7	17,7	17,7	23,7	20,7	20,7	21,7	19,7	19,7	19,7	18,7	23,7
21,7	21,7	21,7	19,7	18,7	25,7	25,7	19,7	25,7	17,7	17,7	19,7	17,7	17,7	15,7

Полученные значения случайной величины называются простой статистической совокупностью.

3.1.1.  Обработка результатов измерений

Для того, чтобы установить закономерность исследуемой величины и ее характеристики, простая статистическая совокупность подвергается обработке, которая заключается в следующем.

1. Все данные располагаются в порядке возрастания или убывания значений случайной величины. Получается так называемый вариационный ряд.

Например, данные приведенного выше примера можно расположить в порядке возрастания нагрузки:

8	13,7	15,7	17,7	18,7	19,7	21,7	22,7	24,7	27,7
9,7	13,7	15,7	17,7	18,7	19,7	21,7	23,7	24,7	27,7
10,7	13,7	15,7	17,7	18,7	19,7	21,7	23,7	25,7	27,7
10,7	14,7	16,7	17,7	19,7	20,7	21,7	23,7	25,7	28,7
11,7	14,7	16,7	17,7	19,7	20,7	21,7	23,7	25,7	29,7
12,7	14,7	16,7	17,7	19,7	20,7	22,7	23,7	25,7	29,7
12,7	15,7	16,7	18,7	19,7	21,7	22,7	24,7	26,7	30,7
13,7	15,7	17,7	18,7	19,7	21,7	22,7	24,7	26,7	32

В вариационном ряде просматривается закономерность случайной величины. Однако при большом числе измерений (порядка сотен) такая форма записи статистических данных становиться громоздкой и мало наглядной.

2. Данные вариационного ряда разбиваются на группы (разряды). Число разрядов зависит от объема выборки. Практика показывает, что в большинстве случаев целесообразно выбирать число разрядов порядка 10 – 20. величина интервала разряда зависит от размаха колебаний случайной величины и минимальных интервалов возможных по различным ограничениям. Проще брать разряды одинаковыми по величине интервала. Крайние значения случайной величины при небольшом числе данных обычно объединяются в один – два разряда с увеличенным интервалом. Величина интервала (с) может быть определена по формуле: