Разработка алгоритма основных состояний и системы управления надежности бесстыкового пути. Расчетное прогнозирование полных отказов и показателей долговечности рельсов. Износ крестовин и сроки службы стрелочных переводов. Расчет вероятности безотказной работы элементов стрелочного перевода, страница 4

   (3.1.)

где x_j^H и  x_j^B    - соответственно максимальное значения случайной величины χ;

К – число разрядов

Например, для вариационного ряда при К = 12, = 32 тс, = 8тс.

Значения случайных величин, совпадающих с границами интервалов, можно условно отнести (для всех разрядов) к первым (в порядке расположения) или вторым разрядом.

3. По вариационному ряду в каждом разряде подсчитывается число наблюдений (частоты), а затем определяются значения частостей:

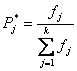,   (3.2.)

где  - частость, выражает статистическую вероятность того, что случайная величина окажется в j-ом разряде;

f_j- частота или число наблюдений в j-ом разряде;

j – номер разряда;

k – число разрядов.

4. Полученные значения разрядов, частот и частостей оформляется в виде статистического ряда, вид которого для рассматриваемой на примере простой статистической совокупности приведен в таблице 3.1.

Таблица 3.1

j	Значения промежутков в разряде xjH - xjB	Частота fj	Частость
1	8-10,7	2	0,025
2	10,7-12,7	3	0,038
3	12,7-14,7	6	0,075
4	14,7-16,7	8	0,100
5	16,7-18,7	11	0,138
6	18,7-20,7	13	0,163
7	20,7-22,7	10	0,125
8	22,7-24,7	9	0,113
9	24,7-26,7	8	0,100
10	26,7-28,7	5	0,063
11	28,7-30,7	3	0,038
12	30,7-32	2	0,025
Итого:		80	1,000

В таблице 3.1 и   обозначают соответственно нижнюю и верхнюю границы j-го разряда. Частость (), например, для первого разряда статистического ряда (таблица 3.1) будет равна

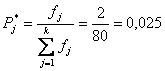
5. Для наглядности статистическое распределение случайной величины часто изображается в виде гистограммы, которая представляет собой графическое изображение статистического ряда и строиться следующим образом: по оси абсцисс откладываются значения интервалов разрядов (Δ x_j) и на каждом из них строиться прямоугольник, площадь которого равна частости ().

Тогда высота прямоугольника (Δ у_j) будет равна

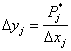  (3.3)

Соединив середины верхних сторон прямоугольников, получим многоугольник распределения случайной величины.

В качестве примера на рис. 3.1 приведены гистограмма и многоугольник распределения по данным статистического ряда (таблица 3.1).

6. По данным статистического ряда определяются числовые характеристики простой статистической совокупности:

а.  Первый начальный момент или статистическое среднее:

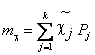    (3.4)

где - среднее значение случайной величины в j-ом разряде статистического ряда

    (3.5)

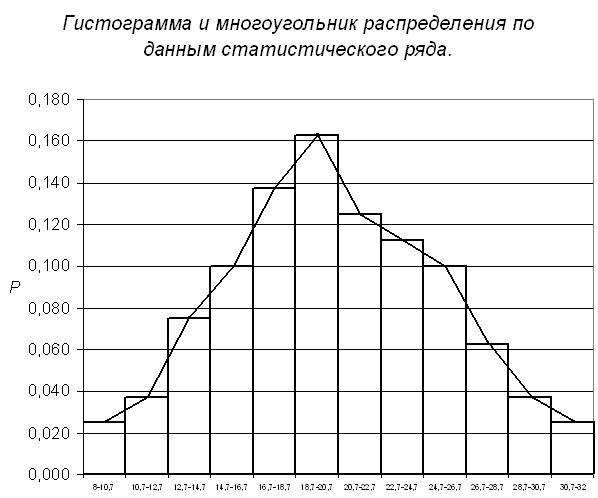
Рис. 3.1.       Гистограмма и многоугольник распределения по данным статистического ряда

б.  Статистическая дисперсия

,   (3.6)

где - статистический второй начальный момент,

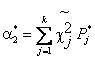  (3.7.)

в.  Статистическое среднее квадратическое отклонение

г.   

  (3.8)

Вычисление числовых характеристик удобно производить, пользуясь табличной схемой, приведенной в таблице 3.2 (для рассматриваемого примера)

Таблица 3.2

j	Значения промежутков в разряде xjH - xjB	Частота Xj	Частость
1	8-10,7	9,35	0,025	0,234	2,186
2	10,7-12,7	11,7	0,038	0,439	5,133
3	12,7-14,7	13,7	0,075	1,028	14,077
4	14,7-16,7	15,7	0,100	1,570	24,649
5	16,7-18,7	17,7	0,138	2,434	43,077
6	18,7-20,7	19,7	0,163	3,201	63,065
7	20,7-22,7	21,7	0,125	2,713	58,861
8	22,7-24,7	23,7	0,113	2,666	63,190
9	24,7-26,7	25,7	0,100	2,570	66,049
10	26,7-28,7	27,7	0,063	1,731	47,956
11	28,7-30,7	29,7	0,038	1,114	33,078
12	30,7-32	31,35	0,025	0,784	24,571
Итого:			1,000	20,4825	445,892

Из таблицы 3.2. следует, что числовые характеристики рассматриваемой простой статистической совокупности будут следующими:

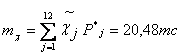
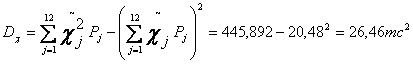
3.2.  Описание алгоритма построения статистического ряда и определения его числовых характеристик

Блок – схема алгоритма приведена на рис. 3.2.

Работа алгоритма начинается с ввода в память компьютера значений числа измерений (n),  числа разрядов статистического ряда (K), любого числа (В) из статистической совокупности (блок  1), а также всех значений (χ_i) статистической совокупности. Затем производится отыскание среди значений статистической совокупности максимального и минимального числа (блоки 6 – 12).

Выражения для определения и имеют вид:

         (3.9)

где = - знак присваивания;

χ_{i –} i-ое значение числа статистической совокупности (i =1,2,…n).

Первоначально идентификаторами x_max и x_min  присваивается значение В (блок 6). Затем содержимое этих ячеек определяется путем последовательной подстановки в правые части выражения их предыдущих значений x_max^’ , x_min^’ и значения числа  χ_i из статистической совокупности.

Так как в математике непредусмотрено деление на нуль, то необходимо произвести проверку на равенство текущих значений и  с χ_i (блоки 7,8). Выбор значений x_max и x_min     произойдет после пересчета по указанным выражениям всех значений χ_i статистической совокупности.

В блоках 13 – 23 производится построение j (j=1,2,….К) разрядов статистического ряда и подсчет в них значений частот  f_{j .}