Характерные особенности: число катушечных групп в фазу равно числу пар полюсов обмотки. Катушечные группы соединяются согласно: конец первой с началом второй… Катушки в группе разной ширины (шага). Отмечу, что длина прямолинейных частей катушек одинаковая, т.к. на практике обмотки лобовых частей всех катушек соединяют вместе в пучок. При чётном числе пар полюсов, в обмотке одинаковое число больших и малых групп.
При нечётном числе p, одна катушечная группа составлена из катушек с одной длинной и короткой сторонами, – «кривая» группа (рис.9)
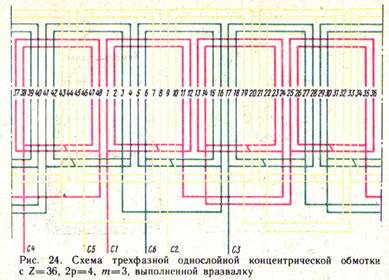
Рис. 9. Рис.10.
При чётном q, можно изменить направление отгиба лобовых частей половины катушек каждой группы – концентрическая катушка вразвалку (трёхплоскостная).
Можно выполнить и не концентрическими катушками, – равнокатушечная или цепная обмотка. У всех катушек одинаковые размеры (рис. 11), поэтому изготовление проще, однако сложнее укладка в пазы.
Рис. 11.
В электрическом отношении обмотки равноценны, но цепные обмотки не применяются в новых машинах из-за сложности укладки.
Бывают катушечными и стержневыми. Применяются: первые в большинстве
машин, вторые – большой мощности.
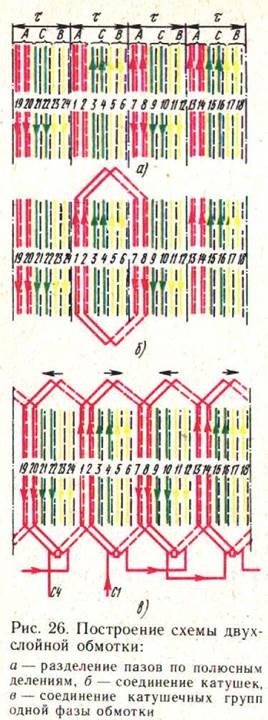
Принцип построения. В каждом пазу – две стороны разных катушек (на рис. 12 верхняя – сплошная линия, пунктир – нижняя). На рис. 12, б показано соединение лобовых частей катушек. Верхние стороны n катушки соединяются с нижней стороной n+6 катушки. Построение иллюстрируется рисунком 12.
Двухслойные обмотки с диаметральными шагами применяются редко, так как укорочение шага позволяет «подавить» 5 и 7-ю гармоники (естественно, не полностью).
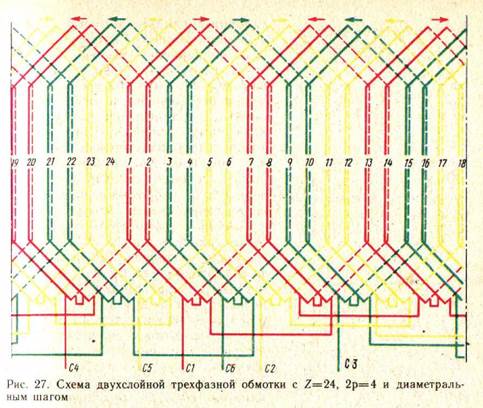
Рис. 12. Рис. 13
Рис. 14.
Часто q=Z/(2pm) выражается неправильной дробью. Так, например, многополюсные синхронные генераторы выполняются с дробным числом пазов на полюс и фазу для улучшения их характеристик.
Обмотки с дробным числом q могут быть соединены в электрически симметричные схемы. Для этого их катушечные группы формируют не из одинакового числа катушек, равного q, как в обмотках с целым числом пазов на полюс и фазу, а из разного; причем в одной части катушечных групп число катушек в группе берут на одну больше, чем в другой. Число малых катушечных групп и число больших катушечных групп подбирают таким образом, чтобы в среднем на одну группу приходилось число катушек, равное выбранному дробному числу q.
Катушечные группы укладывают в пазы в определенной последовательности. Чередование больших и малых катушечных групп повторяется с определенным периодом. Последовательность чередования больших и малых катушечных групп в периоде записывается рядом периодически повторяющихся цифр. Число цифр в периоде показывает, сколько катушечных групп в нем содержится, каждая цифра — число катушек в очередной катушечной группе, а общая сумма цифр — число всех катушек в одном периоде чередования. Для обмотки с q=21/2 таким рядом будет |32|32|32|... Эта запись означает, что в каждом периоде содержится две катушечные группы (две цифры). Первая группа состоит из трех, вторая — из двух катушек. Всего катушек в периоде 3+2=5.
Дробное число q для составления схем записывают в общем виде. так: q = b + c/d= N/d, где b—целая часть числа q; с — числитель; d — знаменатель дробной части числа q; N=bd+c — числитель неправильной дроби, которой можно записать число q.
Количество катушек в малых катушечных группах равно b; количество катушек в больших катушечных группах на единицу больше, т. е. (b+1). В каждом периоде содержится d катушечных групп, из которых с больших и (d—c) малых. Всего катушек в периоде N.
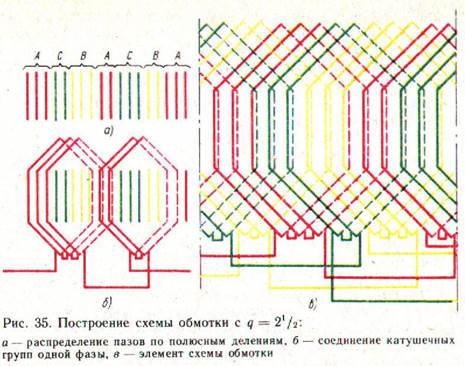
Рис. 15.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.