С учетом того, что при ориентировании вещественных
осей координатных систем (α; β) и (x; y) по вектору ![]() модель
асинхронного двигателя становится аналогичной модели компенсированного
двигателя постоянного двигателя постоянного тока с независимым возбуждением, в
системах векторного управления используется принцип ориентации по вектору потокосцепления
ротора.
модель
асинхронного двигателя становится аналогичной модели компенсированного
двигателя постоянного двигателя постоянного тока с независимым возбуждением, в
системах векторного управления используется принцип ориентации по вектору потокосцепления
ротора.
Для синтеза регуляторов наиболее удобной является модель в системе координат (x; y), т. к. в этом случае координаты модели не содержат гармонических составляющих.
В системах, реализующих принцип прямой ориентации по
полю [5, 14], используются датчики составляющих вектора
![]() . В
качестве датчиков могут быть использованы датчики Холла, а такие специальные измерительные
обмотки, расположенные в воздушном зазоре. Однако в этих случаях возникают проблемы,
связанные с фильтрацией помех, вырабатываемых датчиками. Кроме того,
чувствительность рассматриваемых датчиков зависит от скорости вращения, вследствие
чего на низких скоростях полезный сигнал становится сопоставимым по уровню с
помехами, что затрудняет реализацию системы регулирования.
. В
качестве датчиков могут быть использованы датчики Холла, а такие специальные измерительные
обмотки, расположенные в воздушном зазоре. Однако в этих случаях возникают проблемы,
связанные с фильтрацией помех, вырабатываемых датчиками. Кроме того,
чувствительность рассматриваемых датчиков зависит от скорости вращения, вследствие
чего на низких скоростях полезный сигнал становится сопоставимым по уровню с
помехами, что затрудняет реализацию системы регулирования.
Исходя из изложенного, в современных частотно
управляемых электроприводах для ориентирования вещественной оси координатной
системы по вектору потокосцепления ротора ![]() используется
косвенная ориентация.
используется
косвенная ориентация.
Следует отметить, что системы как прямой, так и
косвенной ориентации обеспечивают точное ориентирование оси α или оси x по
вектору ![]() лишь в
установившихся режимах.
лишь в
установившихся режимах.
Для обоснования условий косвенной ориентации рассмотрим уравнение баланса напряжений в роторе, которое для установившегося режима запишется следующим образом:
![]() .
.
Учитывая, что
![]() ,
,
![]() , получим выражение
, получим выражение
![]() , откуда следует, что
, откуда следует, что
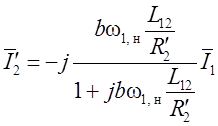 .
.
Следовательно,
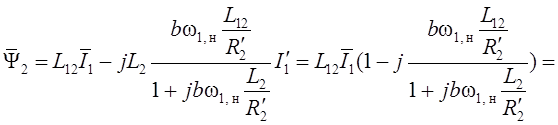
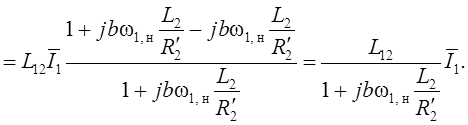
Так как ![]() ,
то
,
то
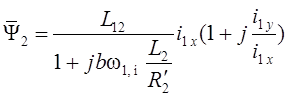 .
.
Если мнимые части числителя и знаменателя будут равны,
то вектор ![]() будет
представлять собой вещественное число, что соответствует его ориентации по
вещественной оси x. Следовательно, равенство
будет
представлять собой вещественное число, что соответствует его ориентации по
вещественной оси x. Следовательно, равенство
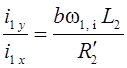
соответствует условию ориентации, откуда
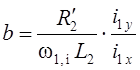 .
.
При построении системы регулирования косвенная
ориентация вектора ![]() по
оси x будет обеспечена, если скорость вращения магнитного
поля всегда будет вычисляться согласно выражению
по
оси x будет обеспечена, если скорость вращения магнитного
поля всегда будет вычисляться согласно выражению
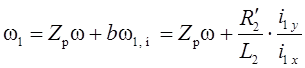 .
.
Аналогичным образом можно показать, что в координатной системе (α; β) условие косвенной ориентации обеспечивается при
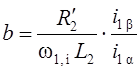 .
.
Поскольку модуль вектора потокосцепления ротора
определяется проекцией ![]() вектора тока статора на ось, связанную
с вектором
вектора тока статора на ось, связанную
с вектором ![]() , а
электромагнитный момент – произведением модуля потокосцепления ротора на вторую
составляющую вектора тока статора, удается построить двухканальную систему
регулирования электроприводом с независимым управлением потокосцеплением ротора
и электромагнитным моментом двигателя. Структурная схема системы показана на
рис. 3.11.
, а
электромагнитный момент – произведением модуля потокосцепления ротора на вторую
составляющую вектора тока статора, удается построить двухканальную систему
регулирования электроприводом с независимым управлением потокосцеплением ротора
и электромагнитным моментом двигателя. Структурная схема системы показана на
рис. 3.11.
Каждый из каналов регулирования строится по принципу подчиненного регулирования в виде двухконтурных подсистем.
Объект управления является нелинейным, в связи с чем синтез регуляторов может быть выполнен лишь приближенно. Окончательная настройка регуляторов производится при наладке электропривода.
Пренебрегая внутренними перекрестными обратными связями, подсистему регулирования потокосцепления представим в виде схемы, показанной на рис. 3.12.
При настройке контуров на технический оптимум найдем:
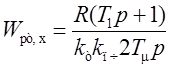 ,
,
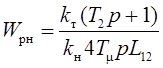 .
.
Канал регулирования скорости представлен на рис. 3.13.
При настройке подсистемы на технический оптимум
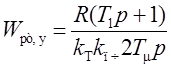 ,
,
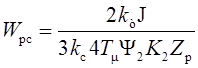 .
.
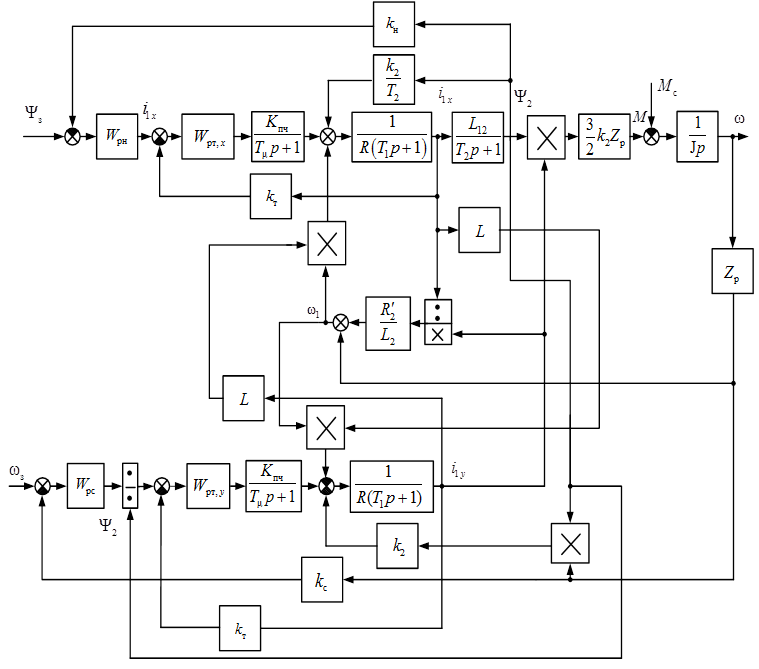
Рис. 3.11. Структурная схема векторного управления
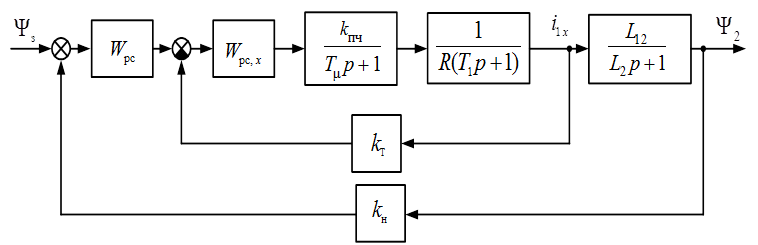
Рис. 3.12. Структурная схема канала
регулирования потокосцепления ротора
Для обеспечения астатизма системы по отношению к нагрузке применяется ПИ-регулятор скорости:
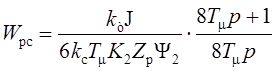 .
.
Функциональная схема электропривода, составленная на основании приведенной на рис. 3.11 структурной схемы, показаны на рис. 3.14 с учетом необходимости координатных преобразований.
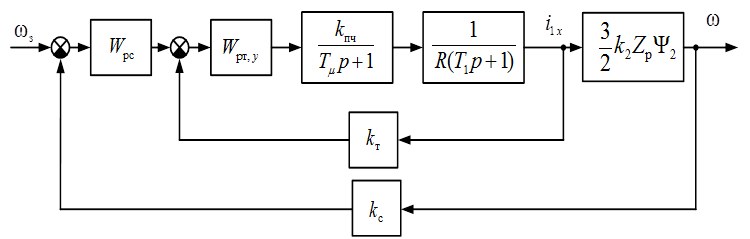
Рис. 3.13. Структурная схема канала регулирования скорости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.