Принципы построения систем частотного управления. Законы частотного управления. Абсолютное скольжение. Схема замещения асинхронного двигателя при частотном управлении, страница 3

3.3. Системы скалярного управления

В рассматриваемых классах систем реализуются законы регулирования (3.1) и (3.2). Системы, реализующие принцип управления в соответствии с (3.1), относятся к наиболее простым. Функциональная схема системы приведена на рис. 3.3. Здесь ЗИ – задатчик интенсивности;  – максимальное значение скорости в заданном диапазоне регулирования;  – наибольшее (допустимое) значение напряжения на входе ПЧ; – число пар полюсов.

Следует отметить, что системы скалярного управления согласно     (3.1) многие производители частотно-управляемых электроприводов называют системами с «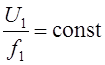» или «вольт-частотным» регулированием.

Системы, основанные на приближенной реализации зависимости    (3.2), могут быть реализованы как в разомкнутом, так и в замкнутом вариантах.

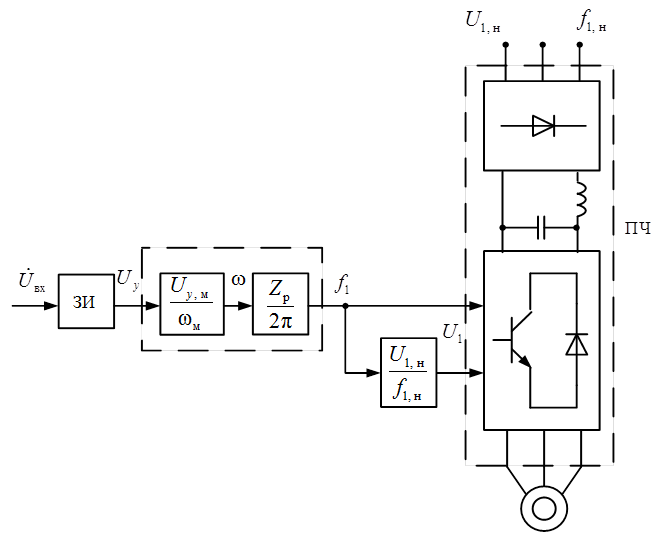
Рис. 3.3. Функциональная схема системы,

реализующей закон регулирования (3.1)

Расчет зависимости c учетом тока статора при наличии нагрузки на валу сложная задача. Поэтому при построении систем, ориентированных на реализацию закона регулирования (3.2), поступают следующим образом. Вначале определяют требуемую зависимость  для режима холостого хода, затем учитывают дополнительное падение напряжения в активном сопротивлении статора от тока статора, вызванного наличием нагрузки на валу.

Из схемы замещения двигателя (рис. 3.1) при b = 0, чему соответствует режим холостого хода, следует, что

Можно потребовать, чтобы обеспечивалось номинальное значение тока намагничивания. Тогда искомая зависимость  запишется следующим образом:

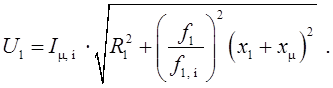                                                               (3.8)

Функциональная зависимость (3.8) представленная на рис. 3.4. Здесь  – значение напряжения при.

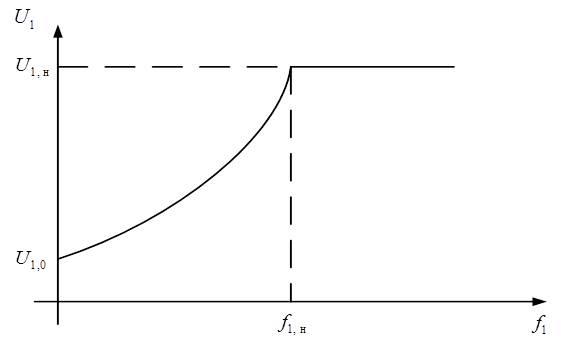
Рис. 3.4. Функциональная зависимость

Значение  можно определить, исходя из выражения:

.

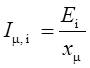Так как , то рассчитываемая зависимость  обеспечивает реализацию закона регулирования (3.2) на холостом ходу, который можно записать также следующим образом:

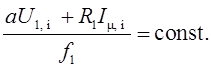                                                                     (3.9)

Схема электропривода, построенная на основе зависимости (3.8)       и реализующая закон (3.2) на холостом ходу приведена на рис. 3.5, где    ФП – функциональный преобразователь, реализующий эту зависимость.

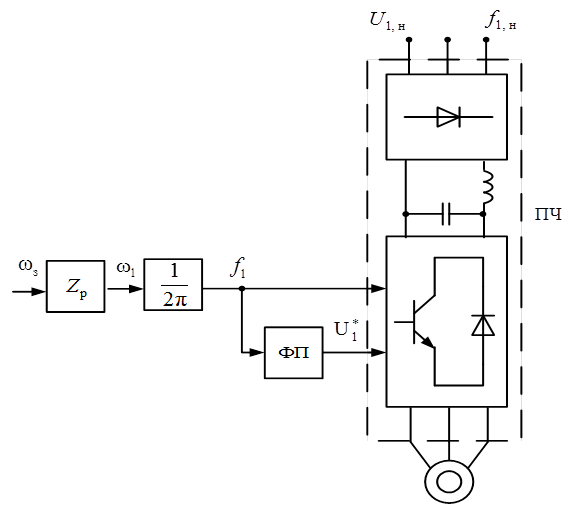
Рис. 3.5. Функциональная схема системы,

реализующая закон (3.2) на холостом ходу

При выводе выражения (3.8) не учитывалась нагрузка на валу двигателя. При наличии нагрузки снижается скорость вращения ротора и увеличивается ток статора. Следовательно, с целью поддержания заданной    скорости вращения, соответствующей частоте , необходимо увеличить частоту, а с целью поддержания условия (3.2) – ввести дополнительную составляющую в добавку к , учитывающую падение напряжения в .

Функциональная схема электропривода с компенсацией скольжения и компенсацией падения напряжения в  при наличии нагрузки на валу приведена на рис. 3.6.

Здесь ФП1 – функциональный преобразователь, реализующий зависимость (3.6); ФП2 – функциональный преобразователь, обеспечивающий дополнительную компенсацию падения напряжения в сопротивлении  при наличии нагрузки на валу; ФП3 – преобразователь, обеспечивающий компенсацию скольжения.

В общем случае коэффициент передачи преобразователя ФП2 может зависеть от частоты и величины тока . Возможен также учет влияния температуры на величину активного сопротивления обмоток статора.        В наиболее простых системах коэффициент ФП2 равен значению  при некоторой температуре нагрева этого сопротивления.

Для пояснения принципа компенсации скольжения рассмотрим схему замещения асинхронного двигателя (рис. 3.1).

Электромагнитный момент, развиваемый двигателем, можно описать следующим выражением [9]:

                                                                                       (3.9)

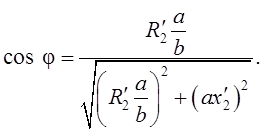
В установившихся режимах двигателях работает при малых скольжениях. Отсюда следует, что коэффициент мощности вторичной цепи близок к единице. Это означает, что ток ротора  соответствует активной составляющей тока статора: