Структурная схема линеаризованной системы,
функциональная схема которой представлена на рис. 3.9, приведена на рис. 3.10.
Здесь ![]() – модуль жесткости механической
характеристики двигателя;
– модуль жесткости механической
характеристики двигателя; ![]() – эквивалентная постоянная времени цепей
статора и ротора.
– эквивалентная постоянная времени цепей
статора и ротора.
Параметры схемы целесообразно определять согласно
[13]: ![]() ,
, ![]() . Здесь
. Здесь ![]() –
критический момент, соответствующий естественной характеристике двигателя;
–
критический момент, соответствующий естественной характеристике двигателя; ![]() – критическое скольжение по естественной
характеристике;
– критическое скольжение по естественной
характеристике; ![]() –
скорость идеального холостого хода по естественной характеристике;
–
скорость идеального холостого хода по естественной характеристике; ![]() – скорость вращения поля при
– скорость вращения поля при ![]() .
.
Передаточной коэффициент преобразователя частоты ![]() определяется
согласно выражению
определяется
согласно выражению
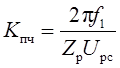 .
.
При однозонном регулировании скорости (![]() )
)
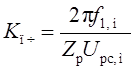 , где
, где ![]() –
максимальное значение выходного сигнала РС. В аналоговых системах регулирования
–
максимальное значение выходного сигнала РС. В аналоговых системах регулирования
![]() В.
В.
Передаточная функция двигателя равна
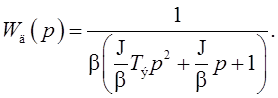 (3. 11)
(3. 11)
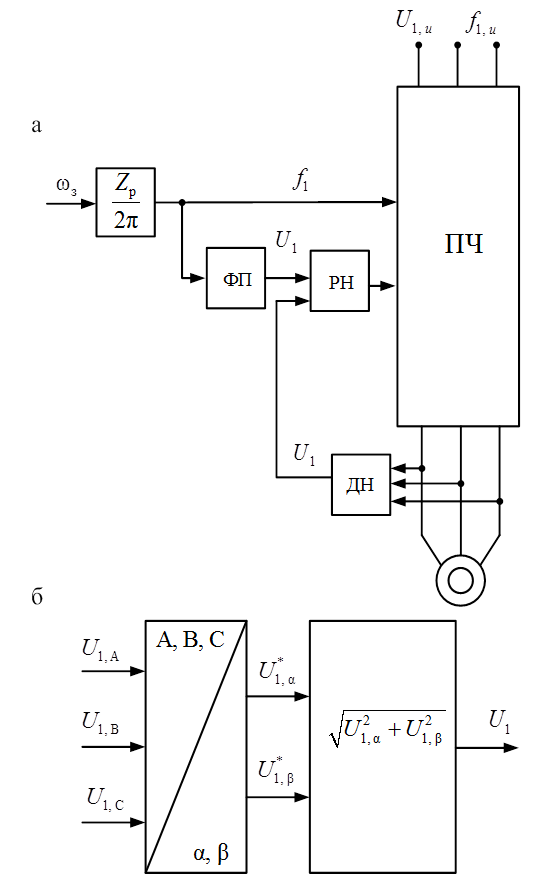
Рис. 3.8. Функциональная схема электропривода
(а) и схема датчика напряжения (б)
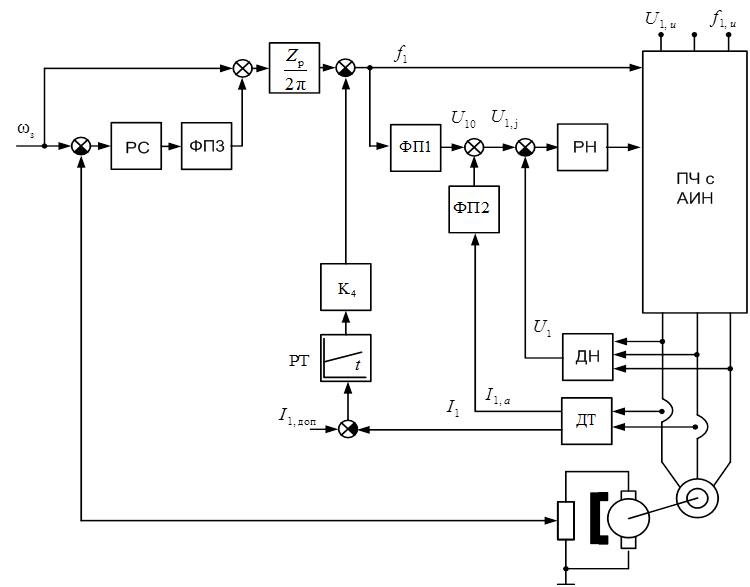
Рис. 3.9. Функциональная схема электропривода
с обратной связью по скорости
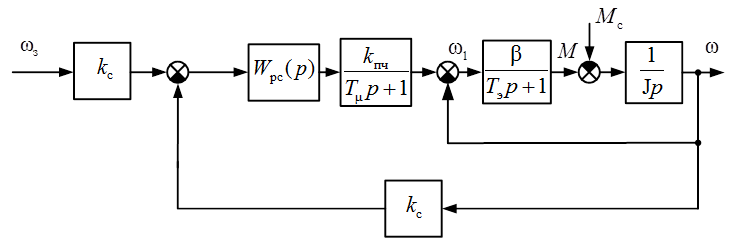
Рис. 3.10. Структурная схема системы регулирования
с обратной связью по скорости
При комплексных полюсах для синтеза регулятора можно принять:
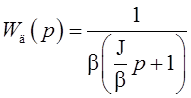 .
.
Тогда при настройке электропривода на модульный оптимум
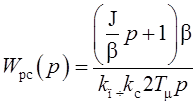 .
.
При вещественных полюсах передаточную функцию (3.11) можно представить следующим образом [14]:
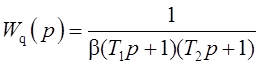 .
.
Здесь
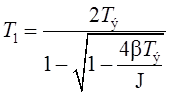 ,
, 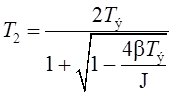 .
.
Постоянную времени ![]() вместе
с постоянной
вместе
с постоянной ![]() можно отнести
к малым некомпенсируемым постоянным. В качестве оценки малых постоянных
можно принять
можно отнести
к малым некомпенсируемым постоянным. В качестве оценки малых постоянных
можно принять ![]() .
Тогда при постройке системы на модульной оптимум
.
Тогда при постройке системы на модульной оптимум
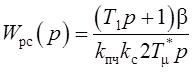 .
.
Системы скалярного управления, реализующие закон регулирования (3.2), обеспечивают поддержание потокосцепления статора в установившихся режимах, что дает возможность поддерживать постоянство перегрузочной способности двигателя независимо от частоты напряжения источника питания двигателя. В то же время значение потокосцепления в переходных режимах существенно изменяется, что снижает динамические показатели качества регулирования.
Отмеченные обстоятельства приводит к тому, что динамические свойства систем скалярного управления уступают соответствующим свойствам электропривода постоянного тока. Этот принципиальный недостаток устраняется в системах векторного управления, называемых также системами с управлением по вектору потокосцепления.
3.4. Системы векторного управления
Согласно [11], векторным частотным называется
управление, при котором вектор напряжения ![]() формируется
путем полной компенсации падения напряжения
формируется
путем полной компенсации падения напряжения ![]() или
или ![]() в
статорных цепях.
в
статорных цепях.
Непосредственная компенсация падения напряжения путем создания положительной обратной связи по току статора связано с необходимостью вычисления производных токов статора, что, в свою очередь связано с трудностями. Поэтому системы векторного управления создаются таким образом, что компенсация создается косвенным путем, за счет поддержания постоянства соответствующего потокосцепления.
Если при изменении частоты в первой зоне регулирования
скорости двигателя напряжение ![]() регулировать
таким образом, чтобы поддерживать соотношения (3.3) и (3.4), автоматически
будет обеспечиваться полная компенсация падения напряжения в сопротивлениях
статора
регулировать
таким образом, чтобы поддерживать соотношения (3.3) и (3.4), автоматически
будет обеспечиваться полная компенсация падения напряжения в сопротивлениях
статора ![]() и
и ![]() .
.
Выполнение соотношения (3.3) будет при этом
обеспечивать поддержание постоянным полного потокосцепления ![]() , а
выполнение условия (3.4) – поддержание потокосцепления ротора
, а
выполнение условия (3.4) – поддержание потокосцепления ротора ![]() .
.
Важной особенностью систем управления, обеспечивающих
поддержание потокосцепления ![]() ,
является возможность прямого измерения
,
является возможность прямого измерения ![]() с
помощью датчиков, установленных в воздушном зазоре двигателя.
с
помощью датчиков, установленных в воздушном зазоре двигателя.
В теории и практике применения систем векторного
управления наибольшее распространение получили системы, обеспечивающие поддержание
потокосцепления ротора ![]() .Такие
системы являются более простыми, чем системы, поддерживающие постоянство
.Такие
системы являются более простыми, чем системы, поддерживающие постоянство ![]() .
Поэтому в дальнейшем остановимся на системах, обеспечивающих регулирование
.
Поэтому в дальнейшем остановимся на системах, обеспечивающих регулирование ![]() , т.
е. реализующих закон регулирования (3.4).
, т.
е. реализующих закон регулирования (3.4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.