Механика грунтов. Физические свойства грунтов. Общие сведения о показателях физических свойств. Примеры решения задач по оценке классификационных показателей грунтов, страница 37

При необходимости более точного определения напряжений при давлениях равномерно распределенных по площади прямоугольных треугольников с другим соотношением сторон, принимается - катет, прилежащий к вершине острого угла; - катет противолежащий

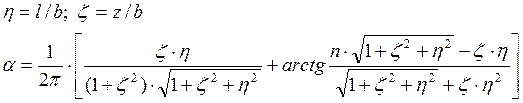
Для практических расчетов напряжения под вершинами в острых углах прямоугольных треугольников с промежуточным соотношением сторон определяются интерполяцией по таблице 10.4.

Напряжения на оси, проходящей через прямой угол треугольника, определяются как сумма напряжений от 2-х прямоугольных треугольников,

10.5. Распределение напряжений от собственного веса грунта.

Случай 1. Основание представлено одним слоем однородного грунта с постоянным весом по глубине (), грунтовые воды отсутствуют.

Случай 2. Основание по глубине представлено несколькими слоями грунта, удельные веса каждого грунтового слоя неизменны, грунтовые воды отсутствуют.

Случай 3. В грунтовом основании, представленном однородным слоем, имеются грунтовые воды, грунт взвешивается .

К расчету принимается двухслойное основание 1   - удельный вес грунта с учетом взвешивающего действия воды.

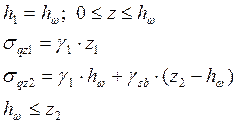
Случай 4. Слоистое грунтовое основание ниже грунтовых вод представлено слоями грунтов, испытывающих () и не испытывающих () взвешивающее действие воды.

10.6. Задания для практических занятий по расчету распределения напряжений в грунте при равномерно распределенной нагрузке на поверхности.

1 – На грунт основания приложена равномерно распределенная нагрузка по площади прямоугольника с размерами . Определить величины сжимающих напряжений по горизонтальным площадкам () и вертикальным площадкам () на вертикальной оси M₁, пересекающей поперечную ось прямоугольника загружения на расстоянии  от его центра. Расчеты выполнить с применением решения задач о действии сосредоточенной силы и способа элементарного суммирования. Изменение глубины положения точек по оси M₁ принять с шагом . Размеры прямоугольника загружения  и интенсивность распределенной нагрузки () принять по таблице 10.5. Построить эпюры напряжений до глубины .

Таблица 10.5

Варианты заданий по нагрузке на поверхности грунта

2 – На грунт основания приложена равномерно распределенная нагрузка () по площади прямоугольника с размерами . Определить величины сжимающих напряжений по горизонтальным  площадкам () на вертикальных осях, проходящих через: центр подошвы прямоугольника загрузки - M₁; угол прямоугольника M₂; внутри площади прямоугольника на расстоянии от угла ; за пределами прямоугольника на расстоянии от угла . Расчеты выполнить с применением метода угловых точек. Изменение глубины положения площадок принять с шагом . Эпюры напряжений построить до глубины . Размеры площади загружения и интенсивность нагрузок принять по таблице 10.5.