|
|
прямоугольник со сторонами
Величины При необходимости величины |
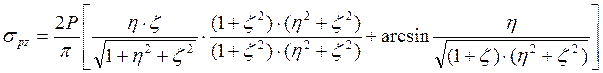
Случай 2, когда вертикальная ось О-О расположена внутри
прямоугольника и не проходит через его центр. Через точку проводятся линии
параллельные сторонам подошвы, прямоугольник условно разделяется на 4-е
прямоугольника со сторонами 
, для
которых точка О является угловой.
|
|
Напряжения по оси О-О на любой глубине z под подошвой прямоугольника определится как сумма напряжений под углами 4-х прямоугольников:
Величины |
Случай 3, когда вертикальная ось О-О расположена за пределами контура прямоугольника загружения. Через точку О и подошву прямоугольника загружения строится прямоугольники, для которых она будет угловой. Напряжения по оси на глубину z ниже подошвы фундамента определяется как сумма напряжений под углами всех условных прямоугольников. Напряжения от загружающих прямоугольников принимаются со знаком плюс «+», а от разгружающих со знаком минус «-».
|
|
Загружающие
прямоугольники:
Величины |
10.3. Распределение напряжений при действии равномерно распределенной нагрузки по полосе (по подошве ленточного фундамента).
Для практических расчетов ленточным считается фундамент (штамп) при
соотношении сторон 
.
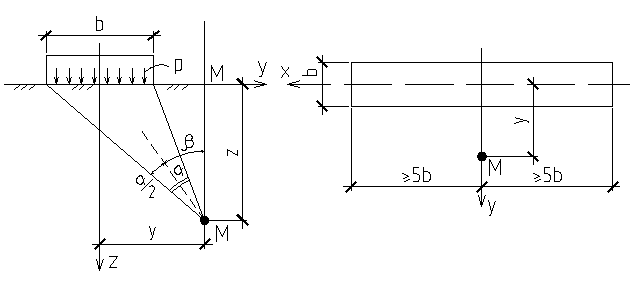
Напряжения на горизонтальных площадках в точке М на глубине z ниже подошвы полосы определяется:
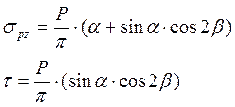
Напряжения на вертикальных площадках в точке М на глубине z определяется:
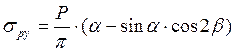
Для практических расчетов напряжений 
под полосовой нагрузкой
принимается табличный метод, аналогично как для прямоугольных фундаментов с использованием
таблицы 10.2 для определения коэффициентов 
под
центром полосовой нагрузки (
).
Случай 1. Ось М-М расположена по средине полосовой нагрузки: (
).
|
|
|
Случай 2. Ось М-М проходит внутри контура полосовой нагрузки (
).
Через точку М проводится линия, разделяющая полосу на
две шириной 
и 
, для которых она лежит на
контуре. Напряжение от каждой условно
|
|
выделенной полосы составляет:
|
принимаются
по табл.10.2 при .
Случай 3. Ось М-М проходит за контуром полосовой нагрузки.
Через точку М производится построение полосы шириной и . Загружение полосы принимается со знаком плюс
«+», полосы шириной со знаком минус
«-».
|
|
|
принимаются по табл.10.2
при .
Для определения суммарного влияния полосовой нагрузки на изменение
напряжений по глубине и простиранию можно
воспользоваться таблицей 10.3
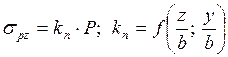, где 
- ширина полосы; 
и 
- глубина и удаление
рассматриваемой точки от центра полосы.
Таблица 10.3
Коэффициент (kn) изменения давлений в толще грунта (σpz) от полосовой нагрузки интенсивностью σpzо=1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
разбивается
на 4-е одинаковых прямоугольника со сторонами 
, для которых точка О
является угловой. Напряжение в любой точке по глубине на оси О-О определяется
как сумма напряжений под углами 4-х равных прямоугольников
принять по
таблице 10.2.
принять по таблице 10.2.
. Разгружающие
прямоугольники: 
. Суммарное
влияние нагрузки определяется прямоугольником 
