Пример 2. Выполнить расчет характерных нагрузок на грунт под ленточным штампом. Площадь штампа принять равной площади штампа в примере 1; А=10 м2. Размеры штампа при η=10: b=1,0м; l= 10,0 м. Характеристики грунта принять из примера 1. Глубины заложения штампа принять как в примере 1.
Решение:
Начальная критическая нагрузка
![]()
- Расчет допустимой нагрузки по условиям применимости принципа линейной деформируемости:
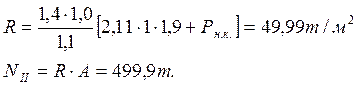
- Расчет критической нагрузки на грунт:
![]()
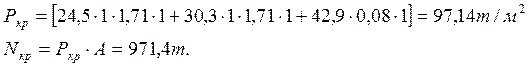
- Расчет допустимой нагрузки на грунт по условиям прочности: γе=1,0; γn=1,15.
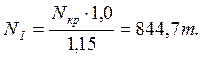
- Сопоставление результатов расчетов в примере 1 и 2, полученных в условиях отличающихся только формой подошвы штампа, показывают расчетные допустимые нагрузки на грунт NII; NI; Nкр под фундаментом прямоугольной формы выше чем под ленточным фундаментом, эта разница увеличивается с уменьшением η. Результаты приведены на графиках рис. 9.4.
Рис. 9.4. Графики сопоставления допустимых нагрузок по условиям II-ой и I-ой групп предельных состояний основания для штампов прямоугольной и ленточной формы в плане при одинаковой площади.
10. Определение напряжений в грунтах.
Определение напряжений в грунтах при действии местных нагрузок от фундаментов зданий и сооружений имеет большое практическое значение для определения деформаций и оценки условий прочности и устойчивости оснований. Напряжения распределяются в массиве грунта на значительную глубину и обеспечивают различные изменения в слоях грунта, составляющих основание. Оценка поведения несущей системы здания требует изучения напряженно-деформированного состояния на значительную глубину в примыкающих зонах грунтового массива.
В механике грунтов при решении вопросов о
распределении напряжений применяют решения теории упругости, которые
справедливы в пределах линейной зависимости изменения деформаций от приложенных
нагрузок. Однако для определения общих деформаций грунтов с учетом одновременно
протекающих как упругих, так и неупругих деформаций, решений теории упругости
недостаточно. Здесь требуются добавочные условия, вытекающие из изучения
физической природы грунтов как дисперсных тел и особенностей их деформирования
под нагрузкой. При определении напряжений в грунтах, они рассматриваются как
линейно деформируемые тела, у которых вся нагрузка передается на скелет грунта,
а ее величина не превышает расчетной допустимой по условиям II-ой
группы предельных состояний (![]() ).
).
10.1. Действие сосредоточенной нагрузки на поверхности полупространства. Способ элементарного суммирования.
- Сосредоточенная нагрузка на поверхности грунта.
|
Рис. 10.1. Схема напряжений на горизонтальной площадке |
|
|
Рис. 10.2. Схема напряжений на вертикальной площадке |
Значения
коэффициентов |
Таблица 10.1
|
|
|
|
|
|
|
|
|
|
0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,20 0,22 0,24 0,26 0,28 0,30 0,32 0,34 0,36 0,38 0,40 0,42 0,44 0,46 0,48 |
0,478 0,477 0,476 0,473 0,470 0,466 0,461 0,455 0,448 0,441 0,433 0,424 0,415 0,405 0,395 0,385 0,374 0,363 0,352 0,3408 0,329 0,318 0,307 0,296 0,284 |
0,50 0,52 0,54 0,56 0,58 0,60 0,62 0,64 0,66 0,68 0,70 0,72 0,74 0,76 0,78 0,80 0,82 0,84 0,86 0,88 0,90 0,92 0,94 0,96 0,98 |
0,273 0,262 0,252 0,241 0,231 0,221 0,212 0,202 0,193 0,185 0,176 0,168 0,160 0,153 0,146 0,139 0,132 0,126 0,120 0,114 0,108 0,103 0,098 0,093 0,089 |
1,00 1,02 1,04 1,06 1,08 1,10 1,12 1,14 1,16 1,18 1,20 1,22 1,24 1,26 1,28 1,30 1,32 1,34 1,36 1,38 1,40 1,42 1,44 1,46 1,48 |
0,084 0,080 0,076 0,073 0,069 0,066 0,063 0,060 0,057 0,054 0,051 0,049 0,047 0,44 0,042 0,040 0,038 0,036 0,035 0,033 0,032 0,030 0,029 0,028 0,026 |
1,50 1,52 1,54 1,56 1,58 1,60 1,62 1,64 1,66 1,68 1,70 1,74 1,78 1,82 1,86 1,90 1,94 1,98 2,00 2,20 2,40 2,60 2,80 3,00 4,00 |
0,025 0,024 0,023 0,022 0,021 0,020 0,019 0,018 0,018 0,017 0,016 0,015 0,014 0,012 0,011 0,011 0,010 0,009 0,008 0,006 0,004 0,003 0,002 0,002 0,000 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.