Лекция 2. Формула полной вероятности. Формула Байеса.
Схема испытаний Бернулли. Случайные величины
Пусть об условиях наступления событияА можно сделать n взаимно исключающих предположений (гипотез) H , H ,...,H1 2 n (т.е. А наступает в совокупности с одной и только одной из гипотез). События H , H ,...,H1 2 n образуют полную группу, следовательно,
n
∑ P H( i ) = 1. Тогда вероятность события А вычисляют по формуле полной вероятности
i=1
(без доказательства):
![]() P A(
) = ∑n
P H(
i
)⋅P
A H(i )
(1)
P A(
) = ∑n
P H(
i
)⋅P
A H(i )
(1)
i=1
Отметим, что в формуле (1) гипотезы H , H ,...,H1 2 n исчерпывают все возможные предположения относительно исходов как бы первого этапа опыта, событие А – один из возможных исходов второго этапа.
Пример 1. В первой урне 2 белых и 1 чёрный шар, во второй − 3 белых и 1 чёрный, в третьей − 2 белых и 2 чёрных. Выбирают наугад одну урну и берут из неё наудачу один шар. Найти вероятность того, что он белый (событие А).
Решение. Об условиях наступления события А (взятый шар оказался белым) можно сделать три взаимно исключающих предположения (гипотезы ): H , H , H1 2 3, где H − шар i был выбран из урны номер i (i = 1 2 3, , ). Таким образом, опыт происходит в два этапа. На первом этапе наудачу выбирают одну из трёх урн с вероятностями
P H( 1)= P H( 2) = P H( 3)=1 3/ , на втором этапе из выбранной урны наудачу берут шар.
![]()
![]()
![]()
![]() Соответствующие условные
вероятности выбрать белый шар при условии, что была выбрана урна номер i (i = 1
2 3, , ),
равны: P A H(1)
= 2
3/ , P A H(
2)
= 3
4/ ,
P
A H(3)=1
2/ . По формуле полной вероятности (1) получим:
P A(
) = P H(
1)P A H(
1)
+ P H(
2)P A H(2)
+
Соответствующие условные
вероятности выбрать белый шар при условии, что была выбрана урна номер i (i = 1
2 3, , ),
равны: P A H(1)
= 2
3/ , P A H(
2)
= 3
4/ ,
P
A H(3)=1
2/ . По формуле полной вероятности (1) получим:
P A(
) = P H(
1)P A H(
1)
+ P H(
2)P A H(2)
+
![]() +P
H( 3)P
A H(3) = (1 3 2 3 3 4 1 2 23 36 064/ )
(⋅ / + / + / )
= / = . .
+P
H( 3)P
A H(3) = (1 3 2 3 3 4 1 2 23 36 064/ )
(⋅ / + / + / )
= / = . .
Формула Байеса
![]() Пусть об
условиях наступления событияА можно сделать n взаимно исключающих
предположений (гипотез) H
, H ,...,H1
2 n , и известно, что в результате опыта событие А произошло.
Вероятность того, что при этом имела место гипотеза H , т.е. P H(A),
где
Пусть об
условиях наступления событияА можно сделать n взаимно исключающих
предположений (гипотез) H
, H ,...,H1
2 n , и известно, что в результате опыта событие А произошло.
Вероятность того, что при этом имела место гипотеза H , т.е. P H(A),
где
k k k =1 2, ,...,n, вычисляют по формуле Байеса (без доказательства):
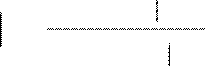 ) P H( )P A H( )
) P H( )P A H( )
![]() P Hk
A =
n k k .
(2)
P Hk
A =
n k k .
(2)
∑ P H( )P A H( ) i i i=1
Пример 2. Пусть при условиях, изложенных в предыдущей задаче, известно, что извлечённый шар − белый, т.е. событие А произошло. Какова вероятность, что была выбрана вторая урна?
Решение. Нужно вычислить
вероятность выбора второй урны при условии, что извлечённый шар оказался белым,
т.е. найти P H(
2![]() A).
По формуле Байеса (2) находим:
A).
По формуле Байеса (2) находим:
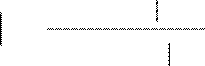 P H(
2
A)
= 3P H(
2)P A H( 2)
= (1 3 3 4/ )
(⋅ / )
=
P H(
2
A)
= 3P H(
2)P A H( 2)
= (1 3 3 4/ )
(⋅ / )
= ![]() 9 = 039. .
9 = 039. .
∑ P H( )P A H( ) 23 36/ 23
i=1 i i
Пример 3. Студент знает 24 билета из 30. В каком случае вероятность вытащить счастливый билет для него больше: если он пойдёт сдавать экзамен первым или если − вторым? Решение. Сравним вероятности двух событий: событие А − вытащить счастливый билет, если он пойдёт сдавать экзамен первым и событие В − вытащить счастливый билет, если он пойдёт сдавать экзамен вторым.
24
P A( )= ![]() =08.
. Вероятность события В зависит от того, какой билет достанется студен
=08.
. Вероятность события В зависит от того, какой билет достанется студен![]()
![]() 30
ту, сдающему экзамен первым. Т.о. об условиях наступления события В можно
сделать два взаимно исключающих предположения (гипотезы ): H1 − студент, сдающий экзамен
первым, вытащил счастливый для второго билет и H2
− студент, сдающий экзамен
первым, вытащил несчастливый для второго билет. P H(
1)=24
30 08/ = . , P H(
2)=6
30 02/ = . . Тогда P B H(1)
= 23
29 079/ = . , т.к в распоряжении
второго студента осталось 23 выученных билета из 29. Аналогично, P B H(2)
= 24
29 083/ = . . По формуле полной
вероятности
30
ту, сдающему экзамен первым. Т.о. об условиях наступления события В можно
сделать два взаимно исключающих предположения (гипотезы ): H1 − студент, сдающий экзамен
первым, вытащил счастливый для второго билет и H2
− студент, сдающий экзамен
первым, вытащил несчастливый для второго билет. P H(
1)=24
30 08/ = . , P H(
2)=6
30 02/ = . . Тогда P B H(1)
= 23
29 079/ = . , т.к в распоряжении
второго студента осталось 23 выученных билета из 29. Аналогично, P B H(2)
= 24
29 083/ = . . По формуле полной
вероятности
(1) находим:
![]() P B(
) = P H(
1)P B H(1)
+ P H(
2)P B H(2)
= 08 079 02 083 08. ⋅ . + . ⋅ . ≈ . .
P B(
) = P H(
1)P B H(1)
+ P H(
2)P B H(2)
= 08 079 02 083 08. ⋅ . + . ⋅ . ≈ . .
Получили P A( ) = P B( ) = 08. , т.е безразлично, кто первым будет сдавать экзамен.
Пример 4. Из ящика, содержавшего 4 белых и 6 чёрных шаров, потеряно два шара. После этого из него наудачу извлекают 2 шара. Найти вероятности событий:
1. Извлечёны чёрные шары.
2. Потеряны шары разного цвета, если известно, что извлечённые оказались чёрными.
Решение. Обозначим: событие В − извлечённые шары оказались чёрными. Об условиях наступления события В можно сделать три взаимно исключающих предположения (гипотезы ): H1 − потеряно 2 белых шара, H2 − потеряно 2 чёрных шара и H3 − потерян 1 белый и 1 чёрный шар.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.