Формула полной вероятности. Формула Байеса. Схема испытаний Бернулли. Случайные величины, страница 6

Плотность вероятности  

Плотность вероятности – один из способов задания закона распределения непрерывной  случайной величины.  Плотностью вероятности f x( )(или плотностью распределения) непрерывной случайной величины  Х  называется производная её функции распределения:

                        f x( ) = F′(x) .                                                                       (6)

Функцию f x( ) называют также дифференциальной функцией распределения. Установим вероятностный смысл этой функции. Из определения производной имеем:

f x( ) = lim F x( + ∆x) − F x( ) .                                          (7)

                                             ∆ →x 0               ∆x

Учитывая равенство (5) : P a( ≤ X < b) = F b( ) − F a( ) , получим из формулы (7), что

f x( ) = _lim ^{P x}( ≤ ^X < ^x + ∆^x) .                                           (8)

                                             ∆ →x 0                ∆x

Плотность вероятности равна пределу отношения вероятности попадания н.с.в. в промежуток [x,x + ∆x) к длине ∆x этого промежутка, когда ∆ →x ⁰. Из равенства (8) следует, что 

                               f x dx( ) ≈ P x( ≤ < +X                               x           dx),                                                   (9)

т.е. произведение f x dx( )   имеет смысл вероятности попадания н.с.в. в дифференциально малый промежуток в окрестности точки x.

Свойства плотности вероятности

1.  f x( )≥0 , т.к это производная от неубывающей функции.

b

2.  P a( ≤ X < b) ⁼ ∫ f x dx( ) .                                                                (10)

a

x

3.  F x( ) ⁼ ∫ f t dt( )   .                                                                              (11) 

−∞

4.  Плотность. вероятности нормирована на единицу:+∞

             ∫ f x dx( ) = 1.                                                                                    (12)

−∞

Пример 5. Дана функция распределения F x( ) непрерывной с.в. Х: 

                0,                 x ≤ 2;

 ²

F x( ) = ax + b, 2 < x < 4;    Найти a, b, f x( ) . Построить графики F x , f x( ) ( ).

                1,                x ≥ 4.



Решение. Параметры a и bнаходим из условия непрерывности F x( ).

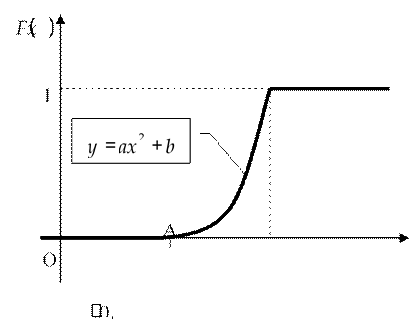
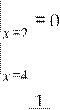Чтобы кривая y = ax² + b проходила соответственно через точки А и В,

                                                                  В                               должны выполняться равенства:

(ax² + b)4a + b = 0

                                                                                                                                ;                           .

                                                                                                            ^_(ax2 + ^b)   = 1 16a + b = 1

4

                                                                                                              Получим a =     , b = − .

                                                                                                                                           12             12

  2                  4                          x

                                                      x ≤ 2;                                               0,          x ≤ 2;

                                                            ′( )x = x ,                                  2 < x < 4;

     F x( ) =      x − 4 , 2 < x < 4;                  f x( ) = F

6

                     1,                    x ≥ ⁴.                                            0,          x ≥ 4.

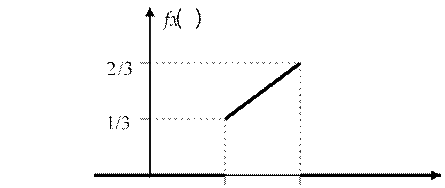
                             0              2             4                            x