С другой стороны такой радиосигнал является периодическим, поэтому его спектр должен быть дискретным с бесконечной шириной спектра. Чтобы проверить это, разложим выражение радиосигнала с гармонической ЧМ, приняв для упрощения обе начальные фазы равными нулю.
После разложения этого колебания в ряд Фурье получим:
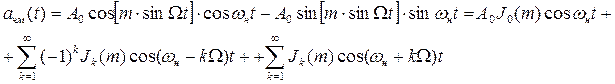
Коэффициенты разложения в ряд Фурье выражены через функции Бесселя к-го порядка от аргумента m.
Из последнего выражения следует, что в состав радиосигнала с гармонической ЧМ входят:
- колебание с несущей частотой ωн и амплитудой А0J0(m),
- бесконечный набор нижних боковых колебаний с амплитудами А0Jk(m) и частотами ωн-kΩ,
- бесконечный набор верхних боковых колебаний с амплитудами А0Jk(m) и частотами ωн+kΩ.
Следовательно, спектр радиосигнала с гармонической ЧМ является дискретным, а ширина спектра в общем случае бесконечна.
Из математики известно, что
функции Бесселя Jк(m)
являются знакопеременными и обладают таким свойством, что их значения
становятся много меньше 1, при k>m+1,
следовательно, в спектре радиосигнала с гармонической ЧМ, ввиду малости, можно
пренебречь боковыми составляющими с номером k>m+1. Значит, число боковых составляющих справа и слева от
несущей будет равно m+1, где m – индекс угловой модуляции,  .
.
Введем понятие практической или действительной ширины спектра ЧМК.
![]() .
.
Оценим среднюю мощность радиосигнала с гармонической частотой модуляции. Для периодическо колебания:
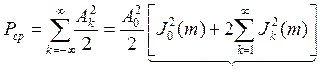
=1 по свойству функции Бесселя.

Выясним, как распределена средняя мощность между составляющими. Можно исследовать два крайних случая: быстрой и медленной ЧМ.
1) Быстрая частотная модуляция, m<<1, Ω>>ωд.
![]()
![]()
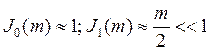

Эффективность модуляции много меньше 1.
При быстрой модуляции распределение мощности энергетически невыгодно. На практике не применяется.
2) Медленная угловая модуляция, m>>1, Ω<<ωд.
![]()
Если учесть, что функция J0(m), определяющая амплитуду несущего колебания, является знакопеременной, то всегда можно подобрать значение m, где J0(m) обращается в ноль, и тогда в спектре будут присутствовать только боковые колебания.
![]()
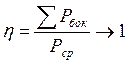 - энергетически
модуляция выгодна.
- энергетически
модуляция выгодна.
Фазовая модуляция.
Если провести анализ спектра радиосигнала с фазовой гармонической модуляцией, то получится такое же разложение, как и при ЧМ. Амплитудные спектры при ЧМК и ФМК одинаковы, отличаются фазовые спектры, следовательно, справедливы все рассуждения о числе учитываемых боковых колебаний и ширине спектра.
![]()
Различие спектра ЧМК и ФМК проявляется при изменении Ω. При медленной угловой модуляции (m>>1):
|
ЧМК Неизменным параметром является девиация частоты: ωд=const (не зависит от Ω)
|
ФМК Неизменным параметром является девиация фазы: φд=m=const (не зависит от Ω)
|

§19. Применение преобразование Гильберта для однозначного определения огибающей, частоты и фазы радиосигнала.
В общем виде любой радиосигнал представляется формулой:
![]() (1)
(1)
Выражение (1) не дает однозначного определения понятий:
А(t) – огибающей радиосигнала,
Ψ(t) – полной фазе радиосигнала.
Можно подобрать бесконечно много
пар параметров А(t) и Ψ(t),
удовлетворяющих уравнению (1). Для однозначного определения этих понятий
условились применять преобразование Гильберта. Преобразование Гильберта для
радиосигнала а(t), будем обозначать![]() .
.
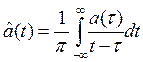 (2)
– прямое преобразование Гильберта;
(2)
– прямое преобразование Гильберта;
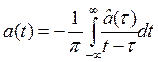 (3) –
обратное преобразование Гильберта;
(3) –
обратное преобразование Гильберта;
![]() (4)
–огибающая радиосигнала;
(4)
–огибающая радиосигнала;
 (5)
– полная фаза;
(5)
– полная фаза;
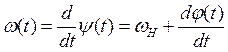 (6);
(6);
![]() -
средняя частота радиосигнала.
-
средняя частота радиосигнала.
Геометрическое представление преобразования Гильберта.
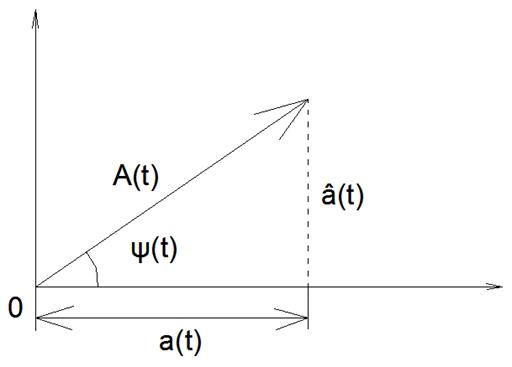
Примеры:
1) Преобразование Гильберта гармонического сигнала:
![]()
![]()
![]()
2) Преобразование Гильберта от суммы гармонических колебаний:
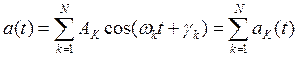
![]()
![]()
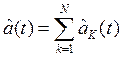
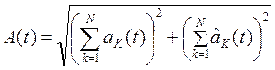

Преобразование Гильберта от суммы гармонических колебаний представляет собой сумму гармонических колебаний с теми же частотами и амплитудами. Фазы этих колебаний отличаются на –π/2. Амплитудный спектр преобразования Гильберта совпадает с амплитудным спектром исходного радиосигнала, а по фазе спектр отличается сдвигом на -π/2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.