Принято называть совокупность
амплитуд гармонических составляющих периодического колебания спектром амплитуд {
Ak }, совокупность фаз гармонических
составляющих периодического колебания спектром фаз ![]() .
Изображают спектр графически в виде спектральных диаграмм.
.
Изображают спектр графически в виде спектральных диаграмм.
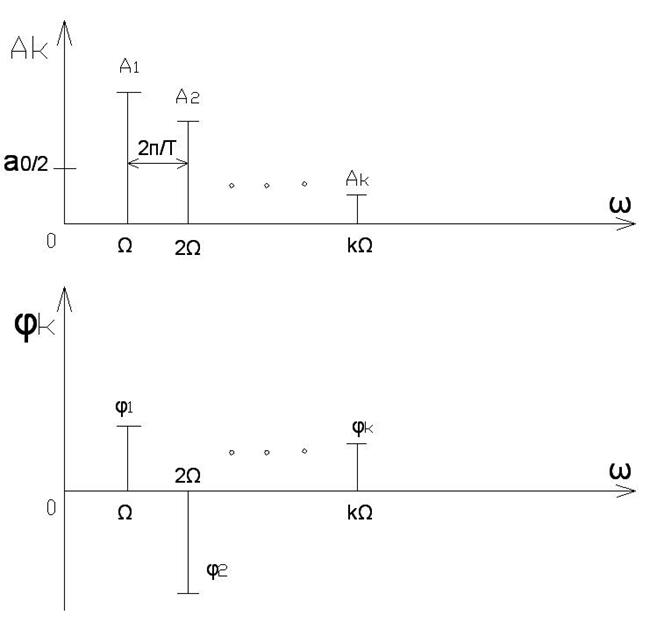
Вывод: спектр периодического колебания всегда линейчатый или дискретный, кроме того этот спектр гармонический, так как частоты всех гармонических составляющих кратны основной частоте Ω.
Найдем среднюю мощность, выделяемую на единичном сопротивлении периодическим колебанием, через коэффициенты разложения в ряд Фурье. Для нахождения средней мощности периодического колебания достаточно найти среднюю мощность этого колебания за период.
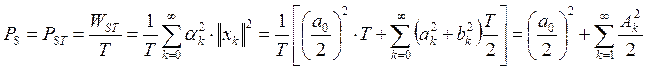 ;
;
 , где
, где
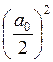 –
средняя мощность постоянной составляющей;
–
средняя мощность постоянной составляющей;
![]() –
средняя мощность k-ой гармонической составляющей.
–
средняя мощность k-ой гармонической составляющей.
Вывод: средняя мощность периодического колебания равна сумме средних мощностей его составляющих.
Заметим, что больший вклад в суммарную мощность вносят гармоники с большей амплитудой.
Особенности спектра периодического колебания.
1. Спектр
дискретный (линейчатый), частоты всех гармонических составляющих кратны основой
частоте 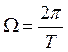 .
.
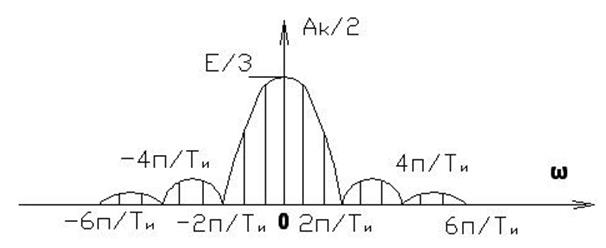
2. В общем случае количество гармонических составляющих периодического колебания бесконечно, то есть ширина спектра периодического колебания бесконечна.
3. Обычно в спектре периодического колебания с увеличением номера гармоники k, амплитуда составляющей уменьшается, следовательно, с увеличением k ее вклад в мощность колебания уменьшается, поэтому в спектре любого периодического колебания можно пренебречь или удалить гармоники, начиная с некоторого kmax. При этом ширина спектра [∆ω] уменьшиться и станет конечной
![]()
§4. Представление периодического колебания рядом Фурье в комплексной форме.
Преобразуем известное разложение в ряд Фурье по тригонометрическим функциям:
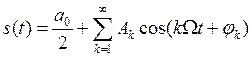 (1)
(1)
где 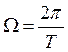 ;
;
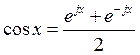 (2)
(2)
С учетом (2) получим:
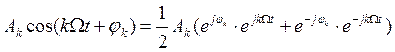

![]() –
комплексная амплитуда k-ой гармонической составляющей.
–
комплексная амплитуда k-ой гармонической составляющей.
![]()
![]()
Представление колебания рядом Фурье в комплексной форме:
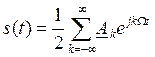 (3)
(3)
При таком представлении считается, что в состав колебания входят гармоники с положительными и отрицательными частотами.
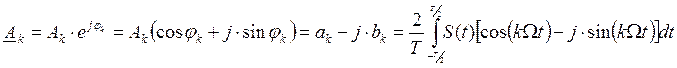

![]()
![]()
При комплексном представлении ряда
Фурье, амплитудные и фазовые спектры периодического колебания становятся
двухсторонними. Амплитуды гармоник с частотами kΩ и - kΩ равны ![]() .
.
На практике можно использовать и односторонние и двухсторонние спектры.
Пример:
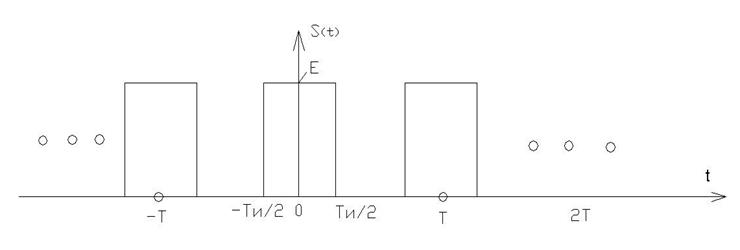

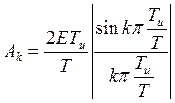
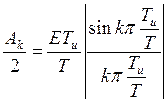
 - среднее
значение (постоянная составляющая).
- среднее
значение (постоянная составляющая).
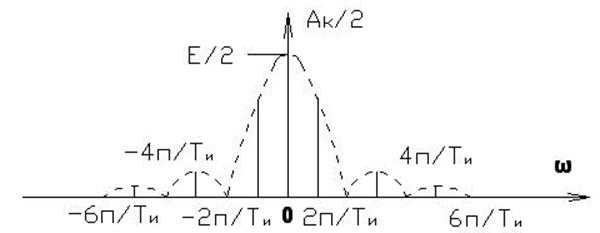
1) Пусть период ![]()
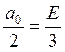
2) ![]()
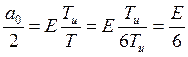
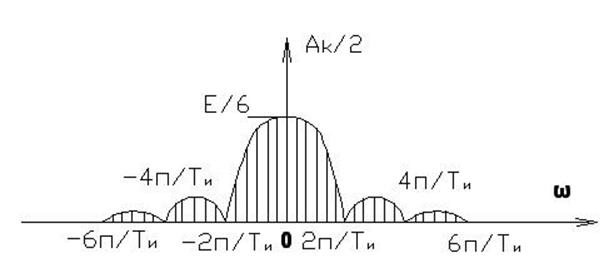
3) ![]()

§5. Спектральный анализ импульсного колебания. Прямое и обратное преобразование Фурье.
Пусть имеется одиночный импульс s(t).

Мысленно (пунктиром) осуществим периодическое повторение этого импульса с периодом Т, для этой периодической последовательности запишем:
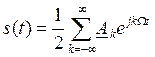 (1)
(1)
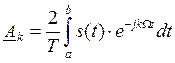 (2)
(2)
Подставим (2) в (1), получим:
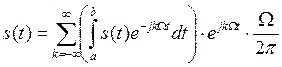 (3)
(3)
Выражение (3) справедливо для нашего импульса лишь на интервале от 0 до Т. При Т→∞, Ω→dω, kΩ→ω, получим:
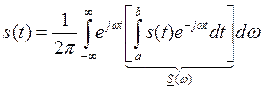
![]() –
спектральная характеристика импульсного колебания.
–
спектральная характеристика импульсного колебания.
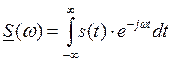 (4)
– прямое преобразование Фурье,
(4)
– прямое преобразование Фурье,
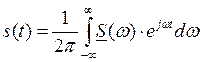 (5)
– обратное преобразование Фурье.
(5)
– обратное преобразование Фурье.
Вместо (4) и (5) договорились писать условное обозначение:
![]()
Спектральная характеристика в
общем случае комплексная функция, а значит у нее есть модуль и аргумент, то
есть ![]() .
.
Выясним физический смысл спектральной характеристики и ее модуля. Сравним выражения (5) и (1):
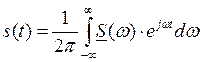 (5)
(5)
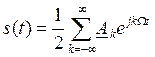 (1)
(1)
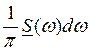 и
и ![]() имеют один и тот же смысл.
имеют один и тот же смысл.
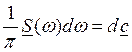 – комплексная амплитуда гармоники с
частотой ω.
– комплексная амплитуда гармоники с
частотой ω.
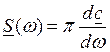 (6)
(6)
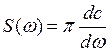 (7) – модуль спектральной
характеристики, его принято называть спектральной плотностью амплитуды.
(7) – модуль спектральной
характеристики, его принято называть спектральной плотностью амплитуды.
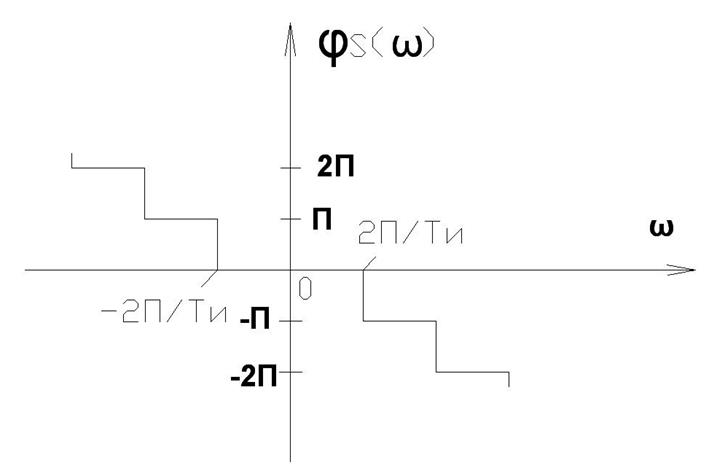
![]() –
фазовый спектр; в отличие от спектров периодического колебания спектры
импульсного колебания являются непрерывными, сплошными.
–
фазовый спектр; в отличие от спектров периодического колебания спектры
импульсного колебания являются непрерывными, сплошными.
Пример: найдем спектральную характеристику импульса
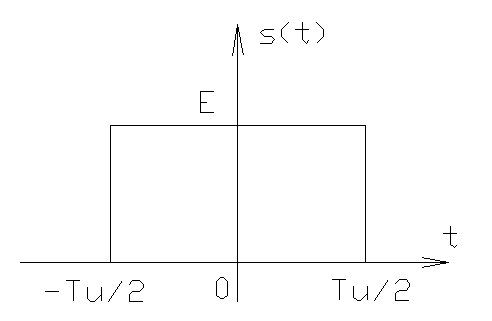
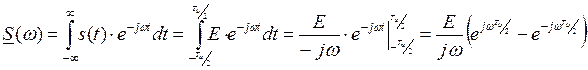
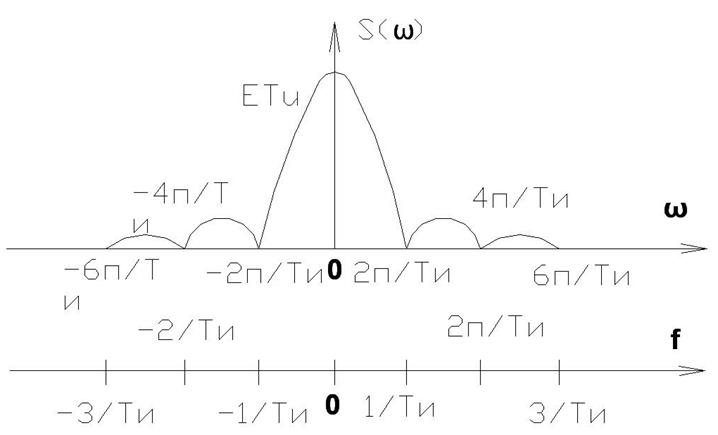
В состав импульсного колебания могут входить гармоники с любыми частотами.
Найдем связь спектра импульсного колебания (одиночного импульса) и спектра периодической последовательности таких импульсов. Для этого сопоставим два выражения
 (2)
(2)
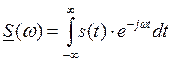 (4)
(4)
Можно сказать:
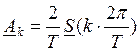 (8)
(8)
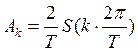 (9)
(9)
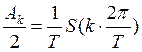 (10)
(10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.