§15. Радиосигнал с АМ несколькими гармоническими колебаниями.
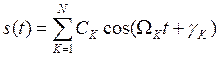
Cк
– амплитуда, ![]() - начальная фаза k-ой
гармоники.
- начальная фаза k-ой
гармоники.
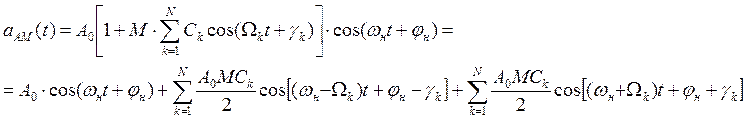
В состав этого радиосигнала входит
гармоническое колебание с частотой ωн, амплитудой А0 и
начальной фазой φн (несущее колебание), набор нижних боковых
колебаний с частотами (ωн-Ωк), амплитудами 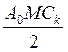 , и начальными фазами (φн-γк) (нижняя боковая полоса); набор верхних боковых
колебаний с частотами (ωн+Ωк), амплитудами
, и начальными фазами (φн-γк) (нижняя боковая полоса); набор верхних боковых
колебаний с частотами (ωн+Ωк), амплитудами 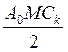 , и начальными фазами (φн-γк) (верхняя боковая полоса). Спектр дискретный.
, и начальными фазами (φн-γк) (верхняя боковая полоса). Спектр дискретный.
ΩN – наивысшая частота модуляции.
Мк – частичный (парциальный) коэффициент глубины модуляции, который характеризует степень влияния гармоники с частотой Ωк на изменение огибающей радиосигнала.
Изобразим спектральную диаграмму этого колебания (б) и спектральную диаграмму управляющего колебания (а).
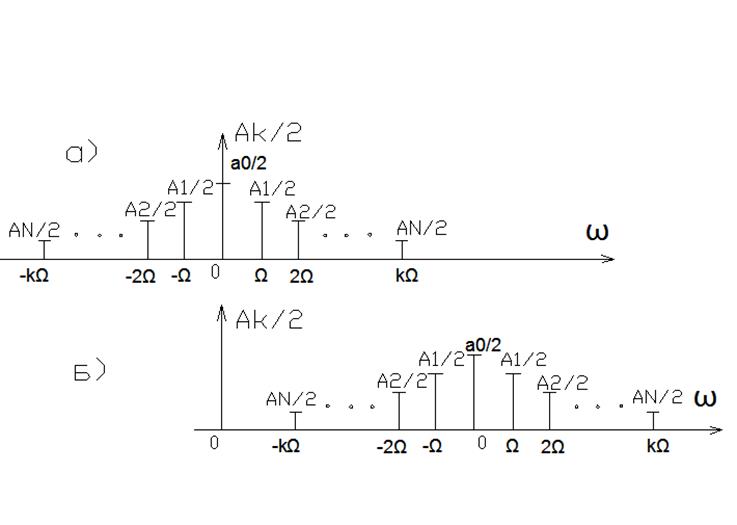
Вывод: ширина спектра АМК при модуляции несколькими гармониками определяется максимальной частотой модуляции и не зависит от того, содержится ли в управляющем колебании гармоники с меньшей частотой.
Форма спектра АМ радиосигнала повторяет форму спектра управляющего колебания. Сам спектр радиосигнала отличается от спектра s(t) сдвигом по оси частот на ωн. Следовательно, при амплитудной модуляции происходит сдвиг в право спектра s(t) на ωн по оси частот.
§16. Радиосигнал с АМ импульсным колебанием.
Пусть ![]()
![]()
Найдем спектральную характеристику радиосигнала:
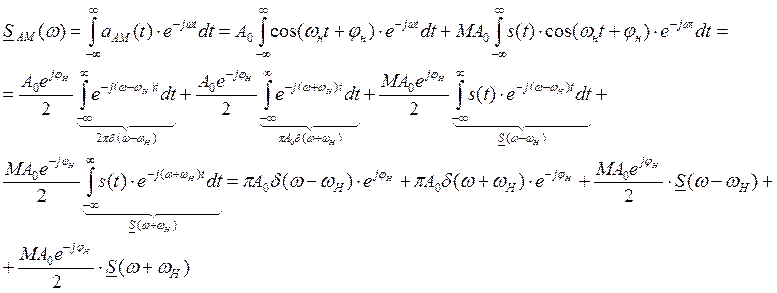
Изобразим модуль спектральной характеристики управляющего колебания (а) и модуль спектральной характеристика радиосигнала с АМ импульсным управляющим сигналом (б).
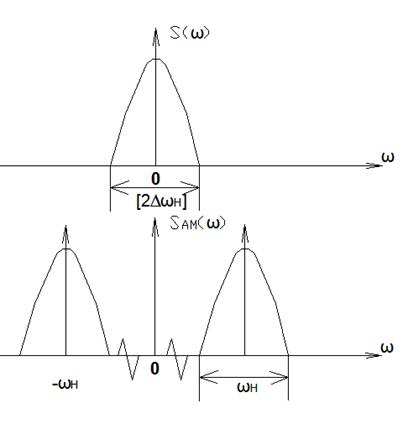
Как видим, ширина спектра такого АМК равна ширине спектра управляющего колебания, а сам спектр радиосигнала смещен относительно спектра управляющего колебания на величину несущей частоты ωн.
§17. Понятие угловой модуляции. ЧМК и ФМК. Радиосигнал с гармонической угловой модуляцией (УМ).
Аналитическое выражение радиосигнала с УМ.
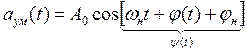 (1)
(1)
При УМ вводится понятие мгновенной частоты сигнала:
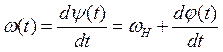
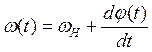 (2)
(2)
Из выражения (2) следует, что при
изменении фазы колебания ![]() меняется мгновенная
частота
меняется мгновенная
частота ![]() . Это позволяет говорить о двух
разновидностях угловой модуляции: частотной и фазовой.
. Это позволяет говорить о двух
разновидностях угловой модуляции: частотной и фазовой.
Условимся считать радиосигнал частотно модулированным, если по закону управляющего колебания меняется мгновенная частота.
![]()
![]() (3)
(3)
ωн – средняя частота радиосигнала,
ωд – коэффициент, учитывающий влияние s(t) на изменение ω(t) – девиация частоты (отклонение от средней частоты).
С учетом выражения (2):
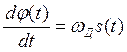
![]() .
.
Как видим, при изменении
мгновенной частоты по закону s(t),
одновременно изменяется и фаза по закону ![]() .
.
Условимся называть фазомодулированным колебанием такой радиосигнал, у которого по закону управляющего колебания меняется фаза.
![]()
![]() (4)
(4)
φд – девиация фазы.
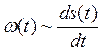 .
.
Как видим, при изменении фазы по
закону s(t), одновременно
изменяется мгновенная частота по закону ![]() /
/
Радиосигнал с угловой гармонической модуляцией.
Угловая гармоническая модуляция будет, когда управляющее колебание гармоническое.
ЧМК.
![]()
![]()
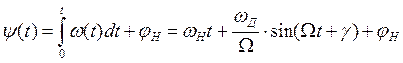
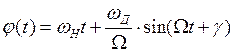
При ЧМ по закону косинуса в радиосигнале существует и ФМ, но по закону синуса.
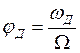 -
девиация фазы.
-
девиация фазы.
Будем обозначать по-другому девиацию фазы:
 -
индекс угловой модуляции
-
индекс угловой модуляции
Аналитическое выражение радиосигнала с гармонической ЧМ по закону косинуса:
![]()
ФМК.
![]()
![]()
Аналитическое выражение радиосигнала с гармонической ФМ по закону косинуса.
![]()
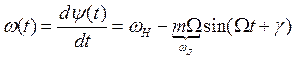
При фазовой модуляции по закону косинуса в радиосигнале присутствует частотная модуляция по закону синуса:
![]()
Как видим, форма радиосигналов с гармонической ЧМ и ФМ совпадает. Отличаются эти колебания лишь сдвигом во времени на четверть периода модуляции.
Заметим, что при любом другом законе модуляции (не гармоническом) формы колебаний ФМК и ЧМК будут различны.
§18. Спектр радиосигнала с гармонической угловой модуляцией.
Частотная модуляция.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Ответ на вопрос о спектре радиосигнала с гармонической ЧМ не является очевидным: с одной стороны мгновенная частота ω(t) меняется непрерывно в пределах [ωн-ωд; ωн+ωд], поэтому можно считать спектр такого радиосигнала сплошным с шириной 2 ωд.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.