Из выражения (10) следует, что модуль спектральной характеристики одиночного импульса и огибающая дискретного амплитудного спектра периодической последовательности этих импульсов, совпадают по форме и отличаются лишь масштабным коэффициентом 1/Т.
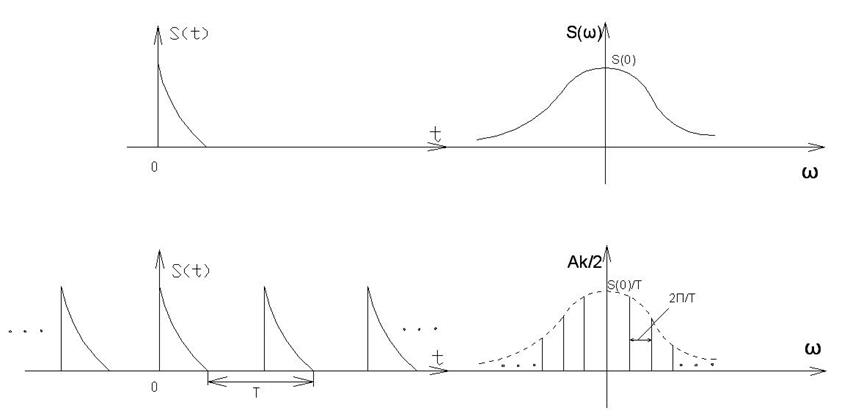
Проверим это на примере последовательности прямоугольных импульсов.
Пример:
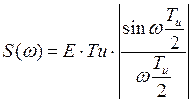
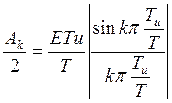
§6. Свойства преобразования Фурье.
Свойства:
1. Спектр суммы колебаний равен сумме спектров этих колебаний. Замечание: под словом спектр мы понимаем спектральную характеристику.
; 
2. Спектр производной импульса:
; 
3. Спектр интеграла:
4. Спектр сдвинутого во времени импульса
τ – координата на оси времени, куда переместился импульс.
5. Сдвиг спектра по частоте:
Сдвинутому по частоте спектру соответствует новый сигнал.
6. Изменение масштаба времени (сжатие – растяжение)
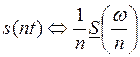
Растяжение сигнала во времени приводит к сжатию его спектра во столько же раз.
7. Спектр произведения двух импульсов равен взятой с коэффициентом 1/2π свертке спектров этих колебаний.
, 
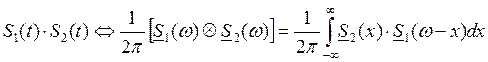
8. Спектр свертки двух импульсов равен произведению спектров этих импульсов.
, где 
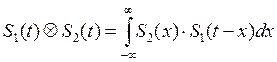
§7. Распределение энергии в спектре импульсного колебания.
Если импульс s(t) представляет собой электрическое колебание, то энергия, выделяемая этим колебанием на сопротивлении в 1 Ом, равна:
Воспользуемся 7-м свойством преобразования Фурье
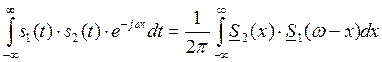
Допустим что:
Пусть ω=0.
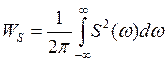, где S2(ω) – спектральная
плотность энергии импульсов, она характеризует распределение энергии импульса
по частоте.
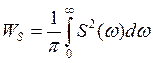
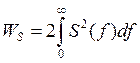
§8. Соотношение между длительностью импульса и шириной его спектра.
Это соотношение определяется 6-м свойством преобразования Фурье
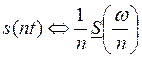
Чем протяженнее сигнал во времени, тем менее протяжен его спектр. Однако само понятие протяженность сигнала во времени (длительность импульса) и протяженность спектра по частоте (ширина спектра) нуждается в уточнении.
Начнем с длительности импульса. Есть импульсы (например прямоугольный, треугольный…) у которых эти понятия определены. Но есть и такие, для которых это понятие не определено.
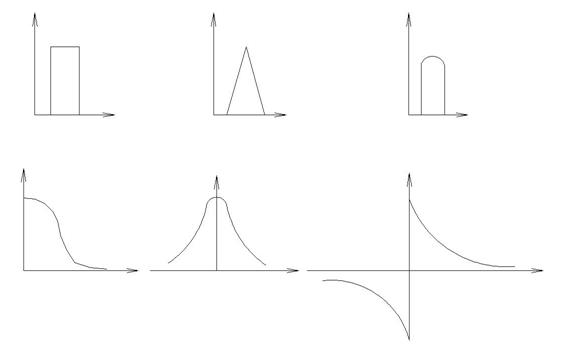
Чтобы получить единообразие в определении длительности импульсов используют энергетический метод, где вводят понятие активной длительности импульса
∆ta – это интервал времени, в котором содержится бóльшая (основная) часть энергии импульса, например, 90%.
Если сигнал (импульс) начинается с нуля, то есть s(t)=0, t<0, то
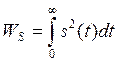
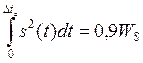
Пример: найти активную длительность импульса прямоугольного импульса.
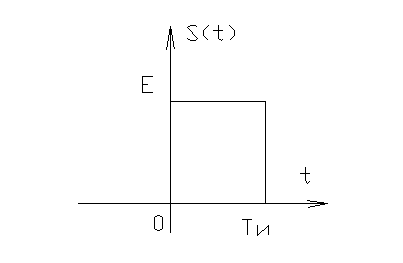
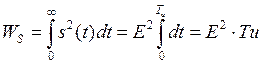
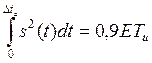
Вводится также понятие активной
ширины спектра импульса [∆ωа] – интервал частот, в котором
содержится основная или большая часть энергии импульса, например, 90%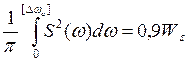 
.
Если вычислить активную длительность импульса ∆ta и [∆ωа] для импульсов различной формы, то выяснится общее для всех импульсов правило:
Как бы мы не изменяли форму импульса, всегда [∆fа].∆ta≥μ, где μ – некоторая постоянная.
Примеры: вычислим спектры различных импульсных сигналов
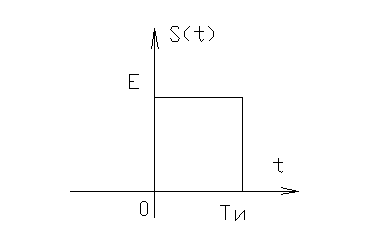
1)
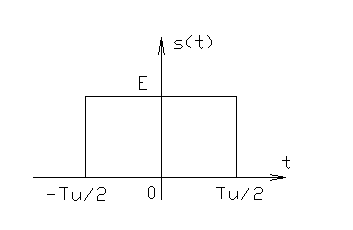
Ранее получено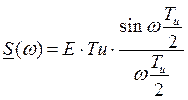 
,
2)
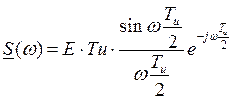
3.
,
.
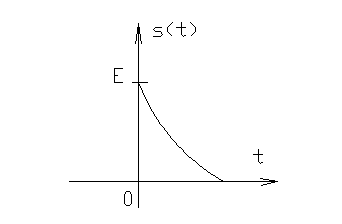
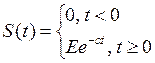
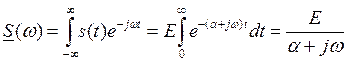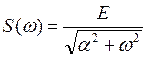4.
,
,
,
,
.
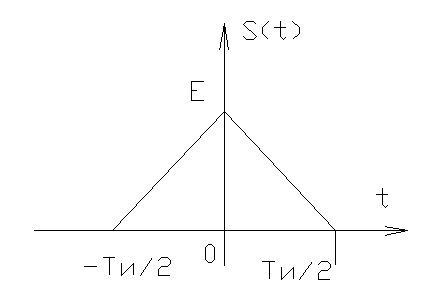
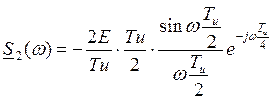
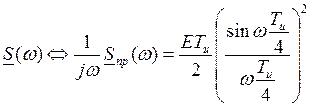
5.
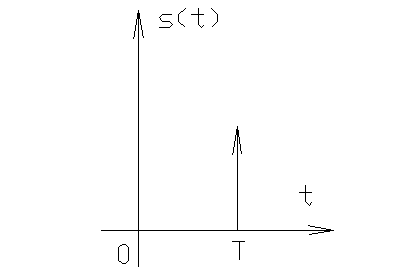
Свойства δ-импульса:
а)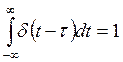 
б)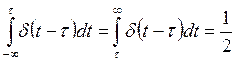 
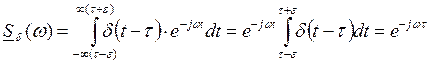, где ε – бесконечная малая
величина.
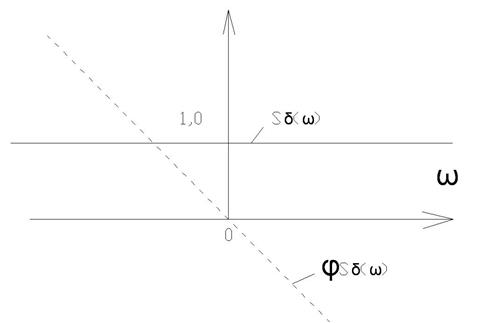
Найдем обратное преобразование Фурье:
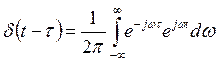
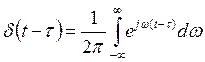
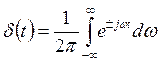
6. Единичный сигнал или функция Хевисайда.
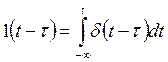
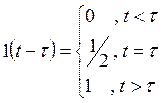
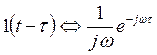
§9. Корреляционный анализ импульсного колебания.
Кроме спектрального анализа в радиотехнике широко используется корреляционный анализ. Введем понятие автокорреляционной функции импульсного колебания s(t) – АКФ, которая характеризует связь этого сигнала с его копией, сдвинутой на время τ, – s(t-τ). Обозначается функция KS(τ).
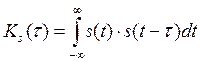
Свойства АКФ:
1. KS(τ)= KS(-τ)
2. KS(0)= WS
3. KS(τ)≤ KS(0), при любом τ.
Примеры:
1)
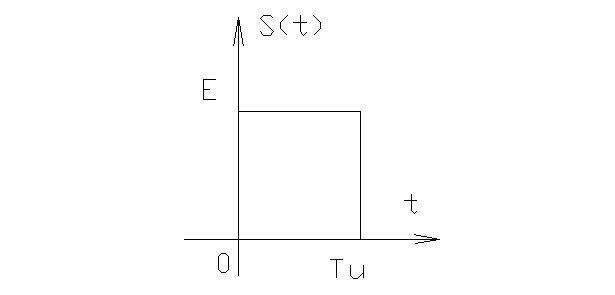
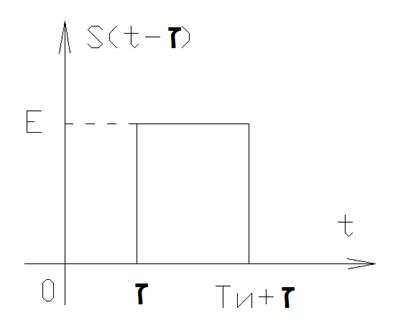
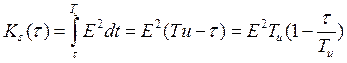
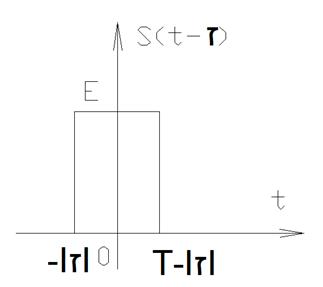
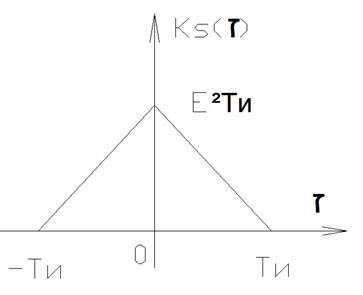
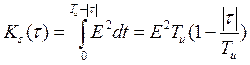
2)
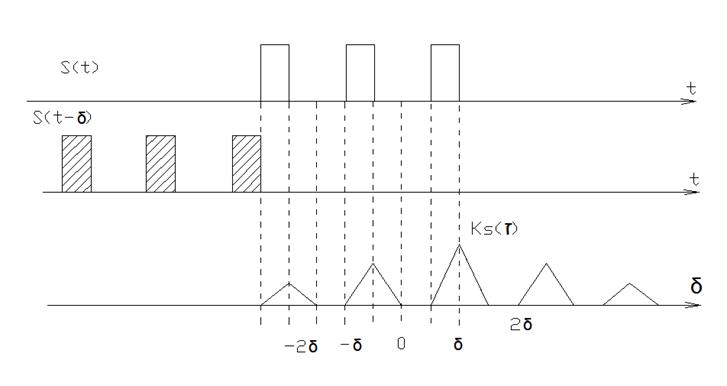
§10. Связь АКФ импульса с его спектральной характеристикой.
Воспользуемся свойством преобразования Фурье.
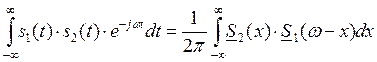
Пусть 
, 
, 
; 
; 
;
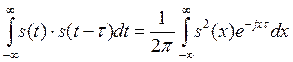
или 
–
спектральная плотность энергии импульса
.
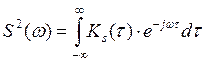На основании свойств преобразований Фурье можно утверждать, что чем протяженнее спектр импульса, тем менее протяженна АКФ, и наоборот.
§11. Понятие взаимной корреляционной функции импульсного колебания (ВКФ).
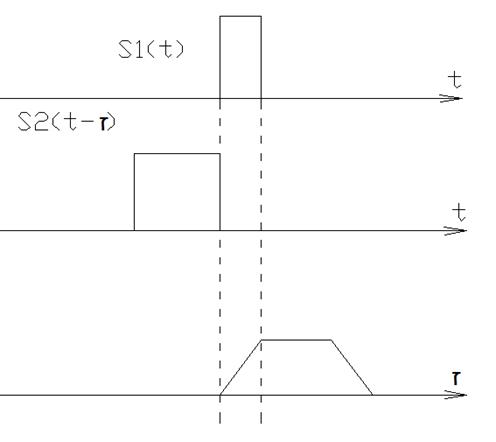
ВКФ характеризует связь импульса s1(t) с копией другого импульса, сдвинутого во времени на τ, s2(t- τ).
У этой функции:
1. не обязательна четность.
2. Не обязателен максимум в 0
Пример:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.