![]() (2)
(2)
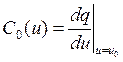 ;
; 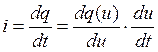 ;
; 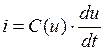 (3)
(3)
Из выражения (3) следует, что при гармоническом напряжении и ток является негармоническим, что свидетельствует о преобразовании спектра сигнала нелинейной емкостью.
Пример: варикап.
в) Нелинейная индуктивность.
Отличительная черта этого элемента нелинейность АВХ (ампер-веберная характеристика).
![]() (4)
(4)
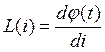 ;
; 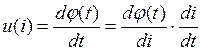 ;
; 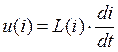 (5)
(5)
Из выражения (5) видно, что при гармоническом токе, напряжение является непериодическим, что свидетельствует о преобразовании спектра сигнала и нелинейных искажениях.
Пример: катушка с сердечником.
У всех нелинейных элементов нелинейные соответствующие характеристики и связанные с этим преобразование спектра сигнала. Поскольку реальные характеристики нелинейных элементов бывают сложными, применяют различные способы их математического описания (аппроксимация характеристик)
Способы:
1) с помощью трансцендентных функций (тригонометрических, экспоненциальных, логарифмических);
2) с помощью степенных полиномов n-ой степени (обычно такую аппроксимацию осуществляют относительно окрестность рабочей точки U0:
![]() );
);
3) аппроксимацию отрезками прямых (кусочно-линейная аппроксимация)
Заметим, чаще всего применяют два отрезка.
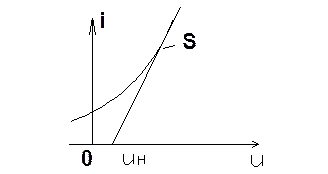
S – крутизна
луча, 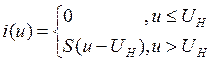
§2. Преобразование спектра сигнала нелинейным резистивным элементом (Аппроксимация ВАХ степенным полиномом).
Аппроксимируем ВАХ нелинейного элемента полиномом n-ной степени:
![]()
1) Воздействие в виде гармонического сигнала
![]()
![]()
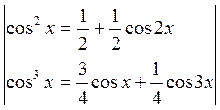
![]()
Из этого выражения следует, что при гармоническом воздействии с частотой ωн на резистивный элемент, ток нелинейного элемента может содержать постоянную составляющую и гармоники с частотами, кратными частоте воздействия kωн, где k=1,2…n.
I1, I2,…,In – амплитуды соответствующих гармоник тока.

Увеличение числа гармоник в спектре называется паразитными гармониками, которые приводят к нелинейным искажениям.
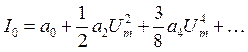

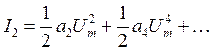

Заметим, что гармоники с частотами не кратными ωн в состав тока входить не могут.
Эффект появления новых гармоник в спектре тока можно использовать для осуществления ряда радиотехнических процессов, например, появление постоянной составляющей можно использовать для операции выпрямления, для этого нужен ФНЧ, пропускающий частоты меньшие ωн. Или же для умножения частоты сигнала (нужно взять полосовой фильтр с полосой пропускания не меньше ωн).
![]() - типовое радиотехническое
звено.
- типовое радиотехническое
звено.
2) Бигармоническое воздействие.
![]()
Подставим в полином
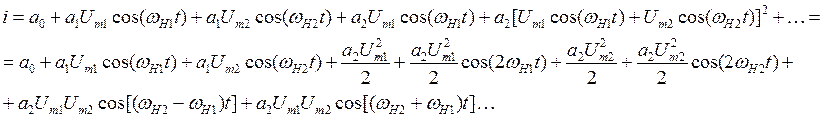
Из этого выражения следует, что при бигармоническом воздействии, ток нелинейного элемента может содержать постоянную составляющую гармонику с частотами воздействия ωн1 и ωн2, гармоники с частотами, кратными kωн1, kωн2, гармоники с комбинационными частотами kωн2±mωн1; k+m≤n.
Амплитудный спектр тока.
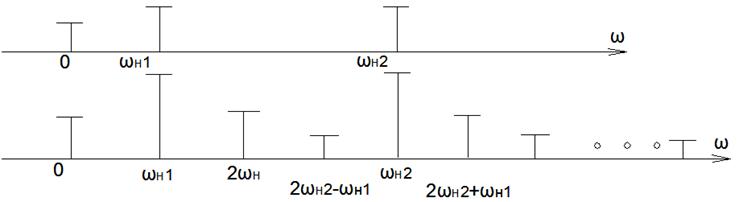
Обогащение спектра тока новыми частотами, с одной стороны паразитное явление, а с другой стороны позволяет получить ряд радиотехнических явлений.
Применение:
а) выпрямление, б) усиление, в) умножение частоты, г) преобразование частоты,
![]()
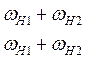
д) модуляция колебания.
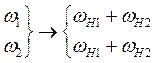
3) Воздействие в виде суммы трех гармоник: АМК с гармоническим законом модуляции
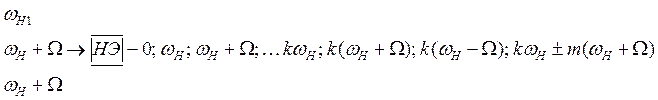 ;
;
а) Выпрямление, б) усиление, в) умножение, г) преобразование, д) модуляция, е) детектирование.
§3. Преобразование спектра сигнала нелинейным резистивным элементом (кусочно-линейная аппроксимация ВАХ).
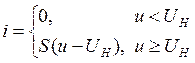
![]()
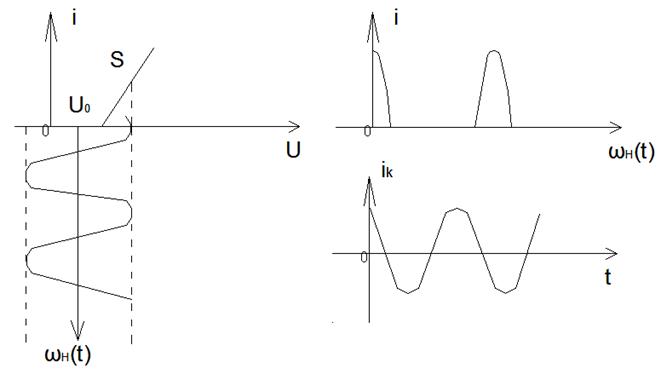
В состав периодического сигнала входит постоянная составляющая и гармоники с чатостами кратными ωн.

![]()
Амплитуды гармоник:
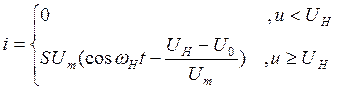 (1)
(1)
при ωнt=0
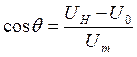 (2)
(2)
Примечание: формулу (2) можно использовать только для нелинейного режима.
Подставим (2) в (1):
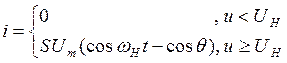 (3)
(3)
Чтобы определить амплитуды отдельных гармоник Ik нужно разложить выражение (3) в ряд Фурье и найти коэффициенты разложения.
![]() (4)
(4)
![]() -
функция Берга.
-
функция Берга.
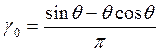 ;
;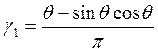
Q – угол отсечки тока (сдвиг по фазе при котором значение от 0 до максимального значения),
imax – амплитуда импульсов тока,
U0 – напряжение смещения,
Uc – напряжение сигнала.
На этом рисунке видно нелинейное искажение гармонического сигнала.
U0=Uн θ=π/2 – нелинейный,
U0>Uн θ>π/2 – нелинейный,
U0≥Uн+Um θ=π – линейный режим работы нелинейного элемента,
U0<Uн θ<π/2 – нелинейный,
U0≥Uн-Um θ=0° – линейный режим работы,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.