Понятие колебания и сигнала. Классификация сигналов.Свойства преобразования Фурье, страница 2

-непрерывные;

-импульсные.

Непрерывные колебания продолжаются бесконечно долго (очень долго). Они обладают бесконечной энергией.

Импульсные колебания отличны от нуля на конечном интервале времени и обладают конечной энергией.

Среди непрерывных колебаний особое место занимают периодические колебания, то есть колебания, значения которых повторяются через равный промежуток времени, которое называется периодом. Среди периодических колебаний очень интересны гармонические колебания.

В-третьих, все колебания можно разделить на:

-не модулированные колебания (несущие), они являются гармоническими;

-управляющие колебания;

-модулированные высоко частотные (ВЧ) колебания (радиосигнал).

Радиосигнал получается путем модуляции несущего сигнала управляющим колебанием.

В-четвертых, все колебания делятся на

-аналоговые;

-дискретные;

-цифровые.

Аналоговые произвольны по величине и непрерывны по времени. Дискретные произвольны по величине, но дискретны по времени, то есть они определены лишь в дискретные моменты времени. Цифровые дискретны и по времени, и по величине.

В радиотехнике обычно применяют довольно сложные сигналы, поэтому для упрощения их анализа удобно представить сложные колебания суммой или линейной комбинацией более простых колебаний.

§2. Разложение колебания по системе ортогональных функций.

При разбиении сложного колебания на более простые составляющие в качестве последних обычно выбирают упорядоченные системы функций, например систему ортогональных функций.

Система вещественных функций  

называется ортогональной, в интервале времени [t₁;t₂], если на этом интервале выполняется условие попарной ортогональности

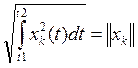 - норма функции х_к(t).

Если нормы у всех функций равны 1, то система функций называется ортонормированной.

Из математики известно, что если функции x_k(t) непрерывные, то произвольное кусочно-непрерывное колебание s(t), удовлетворяющее условию:

может быть представлено суммой

  (1)

где  – коэффициенты разложения.

Принято называть совокупность этих коэффициентов  спектром колебания s(t) в ортогональной системе функций. Заметим, что  полностью определяет колебание s(t).

Если коэффициенты  выбирают в соответствии с правилом

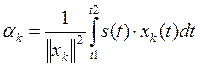 (2), то ряд (1) называют обобщенным рядом Фурье.

Обобщенный ряд Фурье, при заданном числе слагаемых ряда, обеспечивает наилучшую сходимость в смысле средне квадратичного отклонения (то есть оно наименьшее)

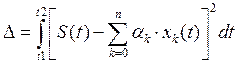  (3)

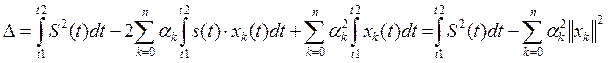  (4)

Систему ортогональных функций называют полной, если при , следовательно, для полной ситемы

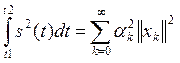 (5)

Если колебание s(t) электрическое, то левая часть равенства (5) представляет собой энергию, выделенную этим колебанием на единичном сопротивлении на интервале времени от t₁ до t₂.

Отсюда следует, что энергия W_S может быть вычислена по коэффициентам разложения

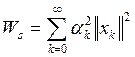  (6)

Средняя мощность колебания s(t) в интервале от t₁ до t₂:

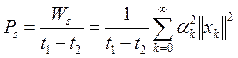
Рекомендации по выбору ортогональных систем функций.

1. Если требуется точное разложение на простейшие составляющие, то выбирается система гармонических ортогональных функций.

2. Если требуется разложение с заданной погрешностью Δ при минимальном числе слагаемых ряда, применяют специальные функции: полиномы Эрмита, Чебышева, Лаггера и т. д..

§3. Гармонический анализ периодических колебаний (разложение периодического колебания в ряд Фурье по тригонометрическим функциям).

Колебание s(t) называют периодическим, если оно удовлетворяет правилу

s(t)=s(t+nT), где ; Т-период.

Периодическое колебание является непрерывным (бесконечно протяженным). Для разложения нужна система функций, ортогональных на интервале времени Т. Этому требованию удовлетворяет система гармонических функций

.

Ряд Фурье в тригонометрической форме:

.

Если колебание s(t) четная функция, то все , если нечетная то  для .

В радиотехнике большее распространение получил другой вариант разложения в ряд Фурье по тригонометрическим функциям:

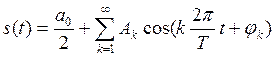 (*), где

     

      .

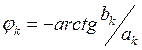Вывод: из выражения (*) следует, что периодическое колебание s(t) может содержать постоянную составляющую  и набор гармонических составляющих с частотами , амплитудами A_k и начальными фазами . Заметим, что никаких других гармонических составляющих, кроме гармонических с частотами, кратными 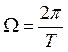, быть не может.