Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 6

3.  Замкнуть ключ К и, приняв момент вспышки за начало отсчета, включить секундомер в момент зажигания лампы. Отсчитав n =10 вспышек, секундомер выключить. Значение времени t занести в таблицу 1.

4.  Повторить п.3 для емкостей 16 мкФ, 8 мкФ, 4 мкФ. Разомкнуть ключ.

5.  Заменить сопротивление R₁ на R₂ = 2,2 МОм и повторить п. 3,4.

IV. Обработка результатов измерений

1.  По формуле 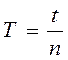   определить период колебаний и занести в таблицу 1. Сделать вывод о зависимости Т от величины R и C.

2.  Определить Z из выражения  (7). Убедиться, что Z есть величина постоянная для данной лампы и при U_ист = const.

3.  Вычислить Z_ср для восьми измерений и Z_ср.

Результат представить в виде:   Z = Z_ср. Z_ср.

Таблица 1.

n = 10
R1 =1,1 106 Ом					R2 =2,2 106 Ом
С, Ф	t, c	T, c	Z	Z	t, c	T, c	Z	Z
	Zср.=                                                Zср.=

V. Вопросы для самопроверки

1.  Что называется релаксацией, временем релаксации, релаксационными колебаниями?

2.  Нарисуйте релаксационные электрические колебания.

3.  Для чего служит конденсатор С в схеме релаксационного генератора (рис.2)?

4.  Как бы выглядела кривая U_C = f (t), если бы неоновая лампа в схеме отсутствовала?

Литература.

1. Калашников С.Г. Электричество. - М.: Наука, 1977. - § 216.

2. Горелик. Колебания и волны. – М.: Физматгиз, 1959. - Гл.4, § 6.

ЛАБОРАТОРНАЯ  РАБОТА  № 22.

ИЗМЕРЕНИЕ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА

I. Цель и содержание работы

Целью работы является определение опытным путем зависимости напряженности магнитного поля соленоида от силы тока в нем, а также установление зависимости изменения напряженности поля вдоль оси соленоида конечной длины от положения выбранной точки.

Линии магнитной индукции, а, следовательно, и линии напряженности магнитного поля соленоида в вакууме или воздухе имеют вид, изображенный на рис.1.

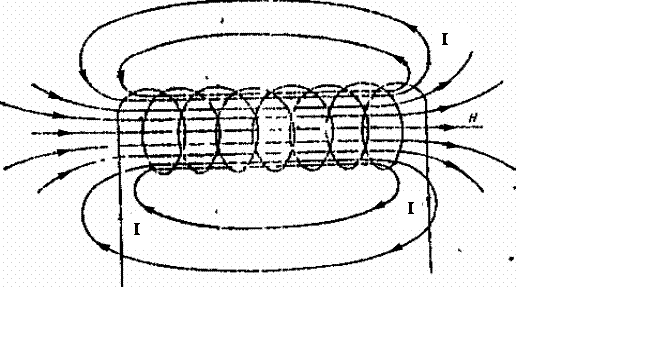
Рис.1

Если длина соленоида во много раз больше диаметра его витков (l >>2R), то поле такого соленоида целиком сосредоточено внутри него, однородно и подобно магнитному полю бесконечно длинного соленоида. В средней части такого соленоида магнитное поле практически однородно и напряженность поля

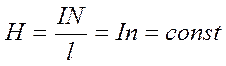 ,                                                                                                                        (1)

где  I  - сила тока, текущего по обмотке соленоида;

l  - длина отрезка бесконечно длинного соленоида;

N  - число витков на длине  l;

n = N / l  - число витков на единицу длины соленоида.

У конечного соленоида напряженность поля вне его  Н ¹ 0, а внутри соленоида поле ослабляется (по сравнению с бесконечно длинным) и становится неоднородным, убывая от его середины к концам.

В середине соленоида напряженность  Н  также оказывается несколько меньшей, чем у бесконечно длинного соленоида с тем же числом витков на единицу длины  n.

В соответствии с законом Био-Савара-Лапласа напряженность магнитного поля для произвольной точки оси конечного соленоида можно выразить равенством

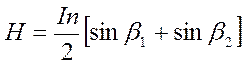                                                                        (2)

или через размеры соленоида (см. рис.2): в центре  │sinβ₁ = sinβ₂ │

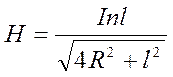                                                                                   (3)

на краю  илиsinb₂