Включение приборов в схему
Амперметр в схему включается последовательно с потребителем энергии.
Вольтметр присоединяется параллельно к тому участку цепи, на котором измеряется напряжение.
Ваттметр имеет две обмотки, включается в схему последовательно-параллельно: обмотка, измеряющая силу тока А, включается в цепь последовательно, а обмотка, измеряющая напряжение на участке цепи Б, - параллельно.
Гальванометр включается в цепь последовательно.
ЛАБОРАТОРНАЯ РАБОТА № 20.
РАЗРЯД КОНДЕНСАТОРА
ЧЕРЕЗ БОЛЬШОЕ ОМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
I. Цель и содержание работы
Цель работы – ознакомление с процессом разряда конденсатора через активное сопротивление. Определение постоянной времени τ = RC.
Конденсатор состоит из двух металлических обкладок, разделенных диэлектриком. Если конденсатор подключить к источнику тока, то на одной из обкладок конденсатора будут накапливаться положительные заряды, на другой - отрицательные.
По мере процесса заряда конденсатора напряжение между его обкладками возрастает, а сила зарядного тока – убывает. Когда напряжение на конденсаторе станет равным напряжению источника, зарядка конденсатора прекратится (следует учитывать, что конденсатор можно заряжать до напряжения, не превышающего предельного, т.е. напряжения, при котором наступает пробой диэлектрика).
Количество электричества, запасенное в конденсаторе, прямо пропорционально его электрической емкости С и напряжению на конденсаторе U: т. е.
q= CU
Если конденсатор отключить от источника тока, а затем обкладки конденсатора замкнуть проводником, то электроны начнут перетекать с отрицательно заряженной обкладки на положительно заряженную, образуя разрядный ток. Скорость разряда зависит от сопротивления соединительного проводника. Если сопротивление мало, то разряд произойдет практически мгновенно; если же велико (порядка миллиона Ом), то сравнительно медленно, и его можно наблюдать с помощью микроамперметра.
Расчеты показывают, что разряд конденсатора происходит по экспоненциальному закону, т.е. за равные промежутки времени сила разрядного тока уменьшается в одинаковое число раз. Допустим, что за каждые три секунды сила тока убывает в два раза, т.е.
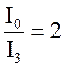 ,
, 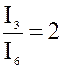 ,
, 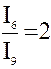 , и
т.д.
, и
т.д.
Логарифмируя эти равенства, получим:
ln![]() – ln
– ln![]() = ln2 = 0,69; ln
= ln2 = 0,69; ln![]() – ln
– ln![]() =
ln2=0,69; ln
=
ln2=0,69; ln![]() – ln
– ln![]() = ln2 =
0,69.
= ln2 =
0,69.
Следовательно, за равные промежутки времени сила разрядного тока уменьшится в одинаковое число раз, а логарифмы тока уменьшатся на одно и то же число, т.е. сила тока убывает в геометрической прогрессии, а логарифм тока – в арифметической прогрессии.
Изменение логарифма тока за единицу времени определяет
постоянную разряда β. Если за время t сила тока уменьшается от ![]() до
до![]() , то
, то
β
= 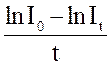 . Отсюда следует, что
. Отсюда следует, что
![]() ;
;  ;
; 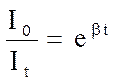 ;
; 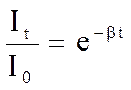 (1)
(1)
Из соотношения (1) следует, что через время t = 1 / β :
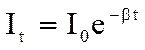 и
и 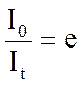 .
.
Т.е. физический смысл величины t = 1/β заключается в том, что она показывает, за какое время сила разрядного тока уменьшается в «e» раз (e ≈ 2,7) . Это время называют постоянной времени τ .
Чем больше величина τ , тем медленнее происходит нарастание или убывание напряжения U на емкости с ростом времени t.
Покажем, что постоянная времени ![]() , где C – электроемкость конденсатора,
, где C – электроемкость конденсатора,
R – сопротивление, через которое происходит разряд.
Сила тока измеряется количеством электричества,
проходящим через сечение проводника в единицу времени 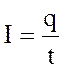 .
При разряде конденсатора сила тока не является величиной постоянной (ток
уменьшается) и
.
При разряде конденсатора сила тока не является величиной постоянной (ток
уменьшается) и 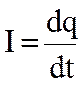 . По отношению к конденсатору dq
есть величина отрицательная (определяет убыль заряда конденсатора) и
. По отношению к конденсатору dq
есть величина отрицательная (определяет убыль заряда конденсатора) и 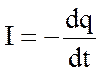 .
.
Так как заряд конденсатора ![]() ,
то
,
то ![]() и
и 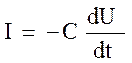 .
.
С другой стороны (по закону Ома) сила разрядного тока
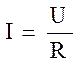 .
.
Приравняем правые части этих равенств, разделим переменные и проинтегрируем
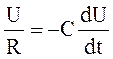 ;
; 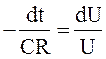 ;
;
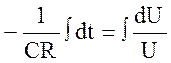 ;
; ![]()
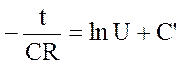
Постоянную интегрирования C’ найдем из
начальных условий. В начальный момент времени (t=0) U = U![]()
![]() и ln U
и ln U![]() = C' .
= C' .![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.