Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 5

- зависимости Т от величины R и C,

- постоянной Z для данной лампы при постоянном напряжении источника (U_ист = const).

Зависимость тока от напряжения для газоразрядной лампы не подчиняется  закону Ома. При малых напряжениях лампа не пропускает ток, т.е. «не горит» (см. рис.1.).

Ток  в лампе возникнет только в том случае, если разность потенциалов на ее электродах достигнет напряжения зажигания    U_заж .

 

Рис.1

При дальнейшем увеличении напряжения сила тока возрастет по закону, близкому к линейному. Если начать уменьшать напряжение на горящей лампе, то при U_заж=U лампа еще не гаснет и ток I продолжает уменьшаться. Лампа перестает пропускать ток при U = U_гаш, которое значительно меньше U_заж. При этом сила тока скачком падает от значения I_гаш до 0. Далее при возрастании U до U_заж и затем уменьшении U до U_гаш процесс повторится.

 

II. Описание лабораторной установки

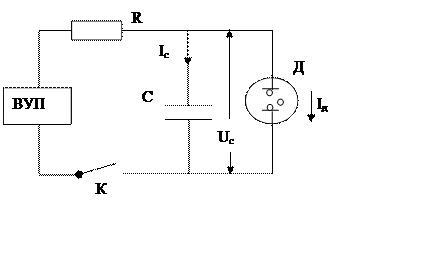
Схема установки представлена на рис.2. Схема включает в себя:

- газоразрядный диод Д;

- магазин емкостей С;

- переменное сопротивление R;

- источник питания – выпрямитель переменного тока ВУП – 2;

- ключ К.

 

 

Рис.2

Исходное состояние схемы: ключ К разомкнут и напряжение на конденсаторе С   U_c = 0.

При замыкании ключа К конденсатор С начнет заряжаться через сопротивление R, и напряжение U_c начнет расти. Как только оно достигнет величины U_заж., лампа начнет проводить ток (т.е. «загорится»). Горящая лампа обладает малым сопротивлением и конденсатор С начнет через нее разряжаться, при этом напряжение  U_c на нем падает. Когда U_c упадет до напряжения U_гаш, лампа перестанет проводить ток и конденсатор С вновь начнет заряжаться, и т.д. Кривая напряжения на конденсаторе С изображена на рис.3.

 

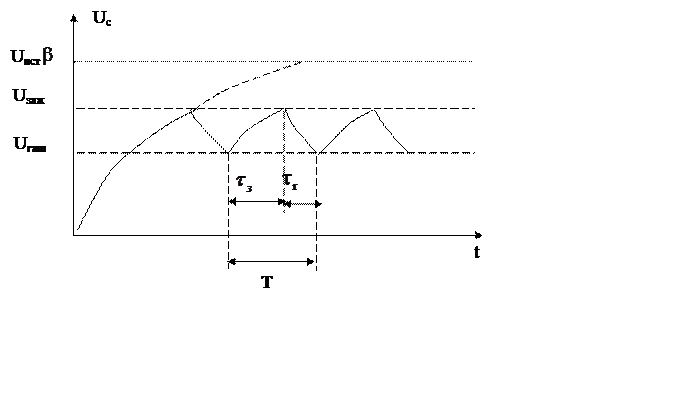Рис.3

Релаксацией называется процесс возвращения в состояние равновесия системы, выведенной из этого состояния.

Мерой быстроты протекания релаксации служит время релаксации, в данном случае – время релаксации контура RC, причем период колебаний Т определяется этим временем. Поэтому колебания рассмотренного типа получили название релаксационных колебаний. При условии, что напряжение источника U_ист. больше U_заж. лампы, для схемы (рис.2) справедливо уравнение:

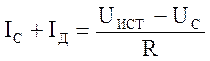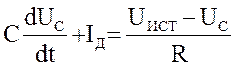   или                                (1)

Вычислим период релаксационных колебаний Т. Полное время одного колебания Т состоит из суммы времени зарядки конденсатора _З  и времени разрядки _Р   (рис. 3). Сопротивление R выбирают существенно большим, чем сопротивление зажженной лампы. Тогда время зарядки конденсатора  _З >>_Р     и   Т = _З +_{Р З}.  Во время зарядки конденсатора лампа не горит ( I_Д = 0), и уравнение (1) примет вид:

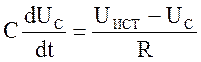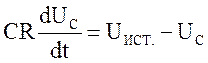   или                                                                                                                            (2)

Будем отсчитывать время с момента гашения лампы, т.е. с U = U_гаш. при t = 0 (рис.3), тогда:

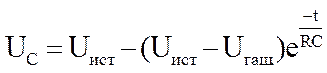                                                                                                                        (3)

В момент зажигания   _З,   _., тогда

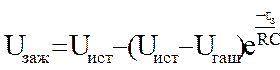                                                                                                                        (4)

Из выражений (3) и (4)

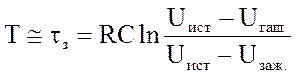                                                                                                                        (5)

Обозначим

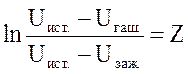                                                                                                                        (6)

Тогда выражение (5) имеет вид                                                                                                                                     (7)

III. Порядок выполнения работы

1.  В качестве R взять сопротивление R₁ = 1,1 МОм.

2.  Установить на магазине емкостей С = 32 мкФ.