Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 19

3. Запишите первое уравнение Максвелла и поясните, что оно показывает?

4. Что такое однородное и неоднородное магнитное поле?

5. От чего зависит магнитная индукция внутри соленоида?

6. Изобразите зависимость напряженности вихревого электрического поля Е от расстояния до оси соленоида.

7. Изобразите зависимость напряженности вихревого электрического поля  Е  от напряженности магнитного поля  Н.

8. Как зависит от частоты напряженность вихревого электрического поля Е?

Литература

1.  Савельев И.В. Курс физики. Т.2. - М.: Наука, 1989.

2.  Ковнацкий В.К. Патент РФ № 2133505. Бюл. № 20 от 20.07.99

ЛАБОРАТОРНАЯ  РАБОТА  № 28.

ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ

 КРУГОВЫХ ВИТКОВ С ТОКОМ

I. Цель и содержание работы.

Цель работы - определение циркуляции вектора напряженности магнитного поля вдоль замкнутого контура, охватывающего и не охватывающего виток с током, и ознакомление с индукционным методом измерения напряженности магнитного поля.

Краткая теория

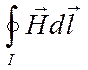Циркуляцией вектора напряженности магнитного поля  Н  вдоль замкнутого контура  l  называется интеграл , где -  вектор, по модулю равный длине  dl  элемента контура и совпадающий с направлением обхода контура.

Циркуляция вектора   по произвольному замкнутому контуру  l  равна алгебраической сумме токов  I_i  , охватываемых этим контуром:

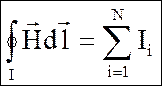,                                        (1)

где  N  – число проводников с током, охватываемых контуром  l.

Если контур  l не охватывает проводники с током, то циркуляция вектора   равна нулю. Уравнение (1) является выражением теоремы о циркуляции вектора  .

В лабораторной работе определяется циркуляция вектора , создаваемого неподвижной катушкой  НК, состоящей из  N  круговых витков, по которым протекает ток  I (рис. 1).

Магнитные силовые линии охватывают проводники с током, лежат в плоскостях, нормальных к проводникам, и всегда замкнуты. На рис. 1 показан случай, когда магнитные силовые линии лежат в плоскости  П, нормальной к  N  проводникам с током  I. Направление магнитных силовых линий и вектора   определяется по правилу буравчика.

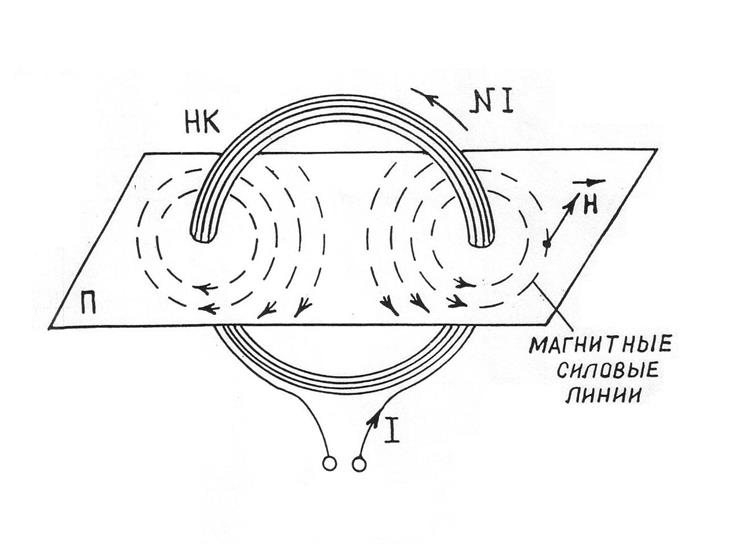
Рис.1

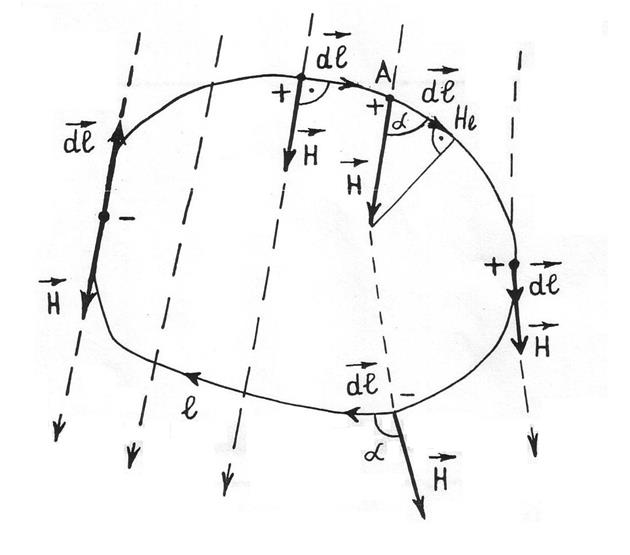
Рис.2

Рассмотрим, каким образом в работе определяется циркуляция вектора  по произвольному замкнутому контуру  l. В точке  А  (рис.2) контура обхода  l вектор   направлен по касательной к магнитной силовой линии (изображена пунктирной линией). Вектор элемента контура  направлен из точки  А  по направлению обхода контура  l.

Циркуляция вектора  по замкнутому контуру

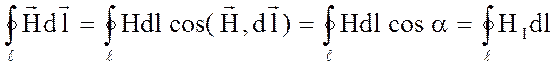,            (2)

где   - проекция вектора   на направление вектора  , α  -  угол между векторами   и .

Если в произвольной точке угол  α ≤ 90°, то проекция  Н₁  положительна, если  α >90°, то проекцию будем считать отрицательной. Знаки проекций определены заранее экспериментальным путем и указаны в каждой точке контура обхода (рис.2).

Интеграл (2) заменим конечной суммой

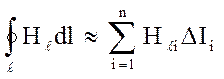,                                     (3)

где  Н_i  -  проекция вектора  на направление  в  i–ой точке,

 - элементы контура конечной длины, соответствующие  i–ой точке.

Элементы контура конечной длины   принимаем одинаковой длины  , тогда циркуляция вектора  по замкнутому контуру определяется по следующему выражению:

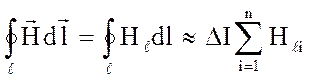                            (4)

Напряженность магнитного поля в произвольной точке контура  l измеряется индукционным методом. Для этого необходимо, чтобы через круговые витки протекал переменный ток.

,                                  (5)

где  I_m  –  амплитуда и  - частота тока. Измеряемая напряженность магнитного поля  Н  на переменном токе будет такой же, как и на постоянном токе  I, если действующее значение переменного тока   будет равно величине постоянного тока  I . Для измерения напряженности магнитного поля в исследуемую точку поместим измерительную катушку  ИК, содержащую  w  витков и имеющую столь малые размеры, что поле в ее окрестности можно считать однородным. Если измерительную катушку  ИК  расположить так, чтобы ось ее (нормаль  ) совпадала с направлением вектора  (рис.3а), то в этом случае амплитуда магнитного потока  , пронизывающего измерительную катушку  ИК, пропорциональна амплитуде переменного магнитного поля   и определяется по следующей формуле: