Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 15

Соленоидом называется цилиндрическая катушка с током, состоящая из большого числа витков проволоки, которые образуют винтовую линию. На рис. 1 изображен соленоид длиной , содержащий N витков с радиусом R. Так как в данном соленоиде выполняется условие L>>R, то его можно приближенно считать бесконечно длинным. Можно также считать, что магнитное поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь. Если к соленоиду приложить гармоническое напряжение, то в цепи будет протекать ток, изменяющийся также по гармоническому закону . Здесь I_m - амплитуда тока,  частота гармонических колебаний, По гармоническому закону с частотой будет изменяться и магнитная индукция в соленоиде:

,                                             (1)

где: B_m - амплитудное значение магнитной индукции.

В дальнейшем будем характеризовать переменное магнитное поле и связанное с ним вихревое электрическое поле соответствующими действующими значениями магнитной индукции B, напряженности магнитного поля Н, напряженности электрического поля Е и ЭДС .

На рис.1 изображены линии магнитной индукции (линии вектора ) в некоторый момент времени и расположенные только в плоскости чертежа.

Из рисунка видно, что во всех точках внутри соленоида векторы магнитной индукцииодинаковы как по модулю, так и по направлению. Такое магнитное поле называется однородным. У концов соленоида линии идут реже и искривляются, а значит, поле становится неоднородным, величина его уменьшается.

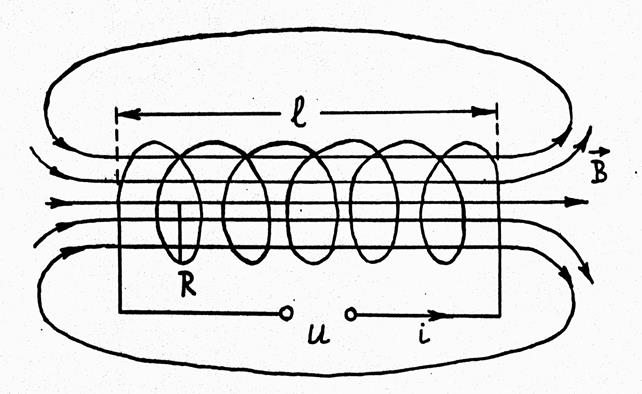
Рис. 1

Согласно Максвеллу, при изменении магнитного поля   во всем окружающем его пространстве возникает вихревое электрическое поле  , силовые линии которого, в отличие от электрического поля, создаваемого зарядом, представляют собой замкнутые кривые. На рис.2 показано вихревое электрическое поле длинного соленоида. Пунктирные линии изображают электрическое поле в момент, когда магнитное поле (сплошные линии) возрастает .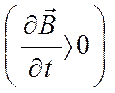

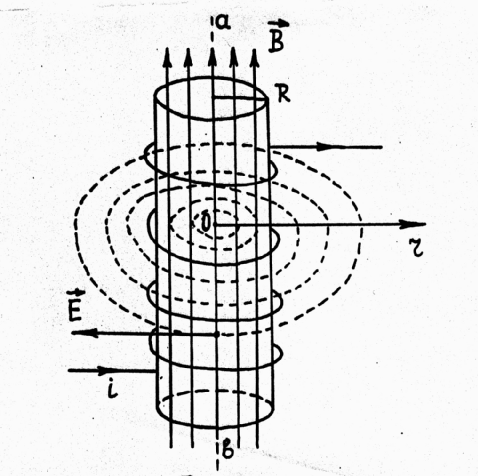
Рис.2

Если замкнутый круговой проводник длиной L поместить в вихревое электрическое поле Е, как показано на рис.3, то оно вызывает движение электронов по замкнутым траекториям и приводит к возникновению ЭДС. Сторонними силами являются силы вихревого электрического поля. Циркуляция вектора Е вихревого электрического поля по замкнутому контуру L равна ЭДС индукции.

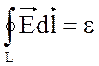                                                     (2)

Вольтметром V с большим входным сопротивлением можно измерить ЭДС в замкнутом круговом проводнике длиной L.

Величина напряженности вихревого электрического поля  зависит от расстояния r до оси соленоида аb (рис.2). Определим эту зависимость для электрического поля внутри соленоида (r<R). Для этого воспользуемся первым уравнением Максвелла [1]:

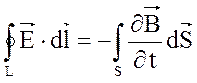                                           (3)

Это уравнение показывает, что циркуляция вектора Е напряжённости электрического поля по произвольному неподвижному замкнутому контуру L, мысленно проведённому в электрическом поле (рис. 4), равна взятому с обратным знаком потоку вектора  через поверхность S, ограниченную этим контуром.

Рассмотрим вначале вихревое электрическое поле внутри соленоида. Преобразуем левую часть выражения (3). Выберем в качестве контура (рис.5) силовую линию вихревого электрического поля внутри соленоида (r<R). Из рисунка видно, что напряженность вихревого электрического поля одинакова во всех точках, равноудаленных от оси соленоида О,  и вектор   направлен по касательной к окружности с центром в точке  О. Тогда циркуляция вектора   по замкнутому контуру

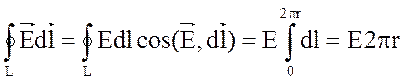                        (4)

Внутри соленоида поле однородно и вектор 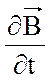 всюду имеет однородное распределение, поэтому правую часть выражения (З) можно преобразовать следующим образом:

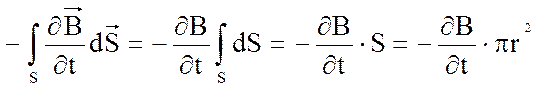          (5)

Учитывая, что магнитная индукция внутри длинного соленоида изменяется по гармоническому закону (1), выражение (5) можно записать в другом виде:

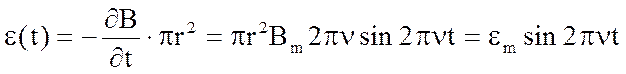   (6)