Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 16

где  (t) - мгновенное, а  - амплитудное значение ЭДС. Соответственно этому, действующее значение ЭДС

                                             (7)

Объединяя выражения (2), (4), (7) и учитывая связь , получим выражение, связывающее напряженность электрического поля Е с напряженностью магнитного поля Н:

                                                 (8)

Из выражения (8) видно, что внутри соленоида (r<R) напряженность электрического поля Е при постоянной напряженности магнитного поля Н и частоте   пропорциональна расстоянию r от оси соленоида (рис.6).

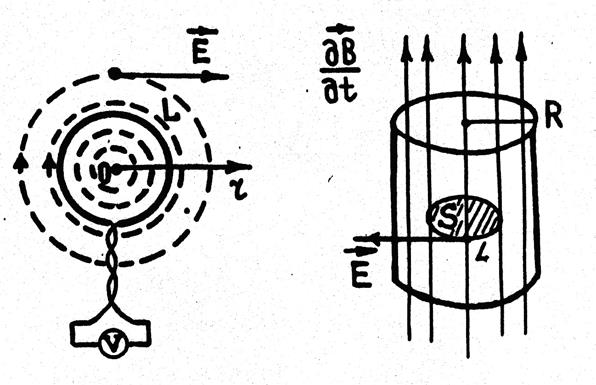
Рис.3                                                   Рис.4

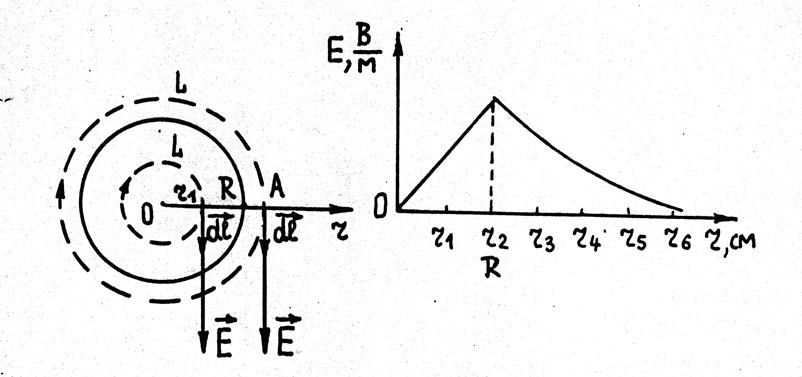
Рис.5                                                   Рис.6

Найдём теперь зависимость напряженности Е вихревого электрического поля вне соленоида от расстояния r до его оси. Выберем точку А (рис.5) вне соленоида на расстоянии r от его оси (rR). Так как переменное магнитное поле внутри соленоида возбуждает в окружающем пространстве электрическое поле, то в силу симметрии силовые линии вихревого электрического поля представляют собой окружности с центром на оси соленоида. Проведем такую окружность через выбранную точку  А. Циркуляция вектора   равна  ЭДС   и определяется выражением (2). Сопоставляя выражения (2) и (4), получим, что напряженность электрического поля в точке  А, расположенной вне соленоида на расстоянии  , равна

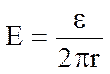                                                   (9)

Из выражения (9) видно, что напряжённость вихревого электрического поля Е вне соленоида () обратно пропорциональна расстоянию r до его оси (рис.4.6).

Для удобства измерения ЭДС вместо одного витка берут плоскую катушку, состоящую из w витков. С учетом этого выражение (9) имеет вид:

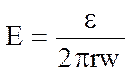                                                  (10)

Если в вихревое электрическое поле поместить плоскую катушку с подключённым вольтметром, как показано на рис.3, то он покажет значение ЭДС, наведённой в катушке. Соответственно, по формуле (10) можно вычислить напряженность электрического поля Е вне соленоида на расстоянии r от его оси.

Если поместить катушку с радиусом r=r₁ внутрь соленоида (r₁<R), как показано на рис.4,5, то напряженность

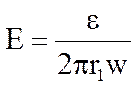                                                     (11)

С другой стороны, напряженность электрического поля Е на расстоянии r₁ от оси соленоида определяется формулой (8):

                                               (12)

Приравнивая выражения (11) и (12), получим формулу для расчёта напряжённости магнитного поля Н внутри соленоида по измеренной вольтметром ЭДС

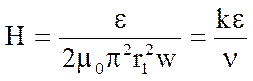,                                   (13)

где 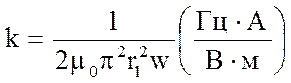- коэффициент, значение которого указано на лабораторной установке.

II. Описание лабораторной установки

Схема лабораторной установки [2] представлена на рис.7, где ДС - длинный соленоид, электромагнитное поле которого исследуется; Г - генератор переменного напряжения; L₁ - подвижная индикаторная катушка; Ш_к - шкала с делениями; Ш- шток, на котором установлена индикаторная катушка L₁ и указатель ее положения У относительно шкалы Ш_к; L₂, L₃, L₄, L₅, L₆ и L₇ - набор неподвижных индикаторных катушек, охватывающих соленоид; П - переключатель индикаторных катушек; V - вольтметр с большим входным сопротивлением для измерения ЭДС, наведённой в соответствующей катушке; А - амперметр.

Под действием переменного напряжения, создаваемого генератором Г, в длинном соленоиде ДС протекает переменный ток, который создаёт в нём переменное магнитное поле. Оно в основном сосредоточено внутри соленоида и носит однородный характер. Вне соленоида магнитное поле настолько мало, что им можно пренебречь.

Согласно Максвеллу, переменное магнитное поле внутри соленоида порождает как внутри, так и снаружи вихревое электрическое поле. С помощью подвижной индикаторной катушки L₁ с радиусом r=r₁ и вольтметра V измеряется ЭДС индукции , наведённая в катушке L₁, а затем вычисляется по формуле (13) напряженность переменного магнитного поля Н, а также по формуле (11) вычисляется напряжённость переменного вихревого электрического поля Е внутри длинного соленоида.