Электричество и магнетизм. Классификация измерительных приборов. Включение приборов в схему, страница 4

Следовательно     –t/СR  =  ln U  –  ln U =  ln      и    U = U e.

Разделив обе части последнего равенства на  R, получим  I = Ie.

Сравнивая соотношения  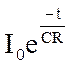   и   I = Ie^–βt,  видим,  что  β  = 1/CR, а CR = 1/β,   что и требовалось доказать.

II. Описание лабораторной установки

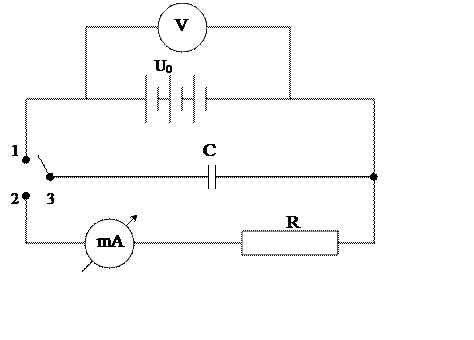
Для выполнения работы собирается схема, показанная на рис.1. Источником тока служит аккумулятор или сухая батарея гальванических элементов Б. Вольтметр V постоянно включен на зажимы источника тока.

Величину напряжения показывает вольтметр V.   С помощью переключателя П  конденсатор может либо включаться на зарядку  (положение 3 - 1), либо замыкаться ( положение 3 – 2) на микроамперметр mА.

 

–                  +

Б

П

Рис.1

III. Порядок выполнения работы

1.  Собрать схему, изображенную на рис.1, (показать преподавателю или лаборанту).

2.  Установить на магазине емкостей  С = 32 мкФ.

3.  Зарядить конденсатор, поставив ключ в положение  3 - 1 ( К1 ).

4.  Подготовить секундомер, перекинуть ключ в положение 3 - 2 ( К2 ) и записывать показания микроамперметра через каждые 10 сек, до  полной  разрядки  конденсатора. 

5.  Измерения, указанные  в  пунктах  3 и 4, произвести  еще  два  раза  и  данные  занести  в  таблицу 1.

6.  Повторить пункты с 3 по 5 для емкостей 16 мкФ и 8 мкФ  и данные занести в табл.2 и табл.3.

7.  Записать значение напряжения источника тока U.

IV. Обработка  результатов  измерений

1.  На миллиметровой бумаге в разумном масштабе по данным опыта построить график зависимости силы разрядного тока  I  от времени. За силу тока  I  взять среднее значение трех измерений.

2.  Найти площадь, ограниченную графиком (за единицу измерения взять квадрат со стороной 5мм).

3.  Найти количество электричества (в микрокулонах), соответствующее одному такому квадрату ( ∆q = I∆t ), и по числу квадратов, ограниченных графиком, найти количество электричества, которое было в конденсаторе до его разряда.

4.  Зная напряжение на конденсаторе (напряжение источника тока) и заряд конденсатора, найти его электроёмкость (в мкФ) и сравнить с ёмкостью, указанной на конденсаторе.

5.  Из соотношения 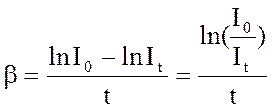найти постоянную разряда β. За время t можно взять время, в течение которого сила тока уменьшилась вдвое.   В этом случае      .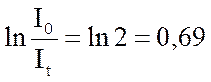

6.  Зная постоянную разряда β и ёмкость конденсатора С, найти сопротивление  R  ( β = 1/CR ).

Таблица 1.

U =
t	I	I	I	Iср
c	мкА	мкА	мкА	мкА
0 10 20 30 40 50 60

Таблица 2.

U =
t	I	I	I	Iср
c	мкА	мкА	мкА	мкА
0 10 20 30 40

Таблица 3.

U =
t	I	I	I	Iср
c	мкА	мкА	мкА	мкА
0 10 20

 

V. Вопросы для самопроверки

 

1.  Что представляет собой конденсатор?

2.  Что является основной характеристикой конденсатора?

3.  В каких единицах измеряется ёмкость конденсатора?

4.  Чем определяется ёмкость конденсатора?

5.  Какие типы конденсаторов вы знаете?

 

Литература

Савельев И.В. Курс общей физики. Т.2, 3.3-3.4. - 2003.

ЛАБОРАТОРНАЯ РАБОТА. № 21.

ИЗУЧЕНИЕ РЕЛАКСАЦИОННЫХ КОЛЕБАНИЙ

 В СХЕМЕ С ГАЗОРАЗРЯДНОЙ ЛАМПОЙ

I. Цель и содержание работы

Цель работы – определение:

- периода релаксационных колебаний Т при различных значениях R и C,