МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Теория рынка»
ОСНОВЫ ЭКОНОМЕТРИКИ
(Раздел 3. парная регрессия)
теоретические материалы для студентов ОФиП
Новосибирск, 2008
3. МОДЕЛЬ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
3.1. Постановка задачи
Пусть имеются наблюдения за двумя признаками: X и Y. Допустим, что проведенный ранее корреляционный анализ показал наличие значимой линейной связи между этими признаками. Каждое i-е наблюдение можно изобразить на плоскости (X,Y) в виде точки с координатами (x yi, i), как это представлено на рис.5. Наша задача будет состоять в том, чтобы найти такое уравнение линейной зависимости, которое бы «наилучшим образом» описывало исходные данные.
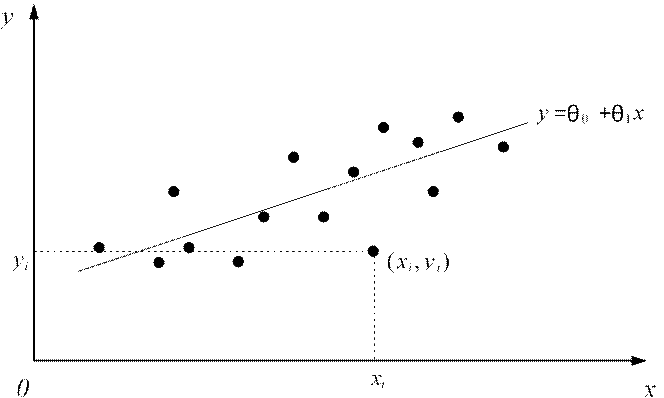
Рисунок 5. Графическое представление исходных данных при построении парной регрессии
Для определенности будем считать, что Y – это зависимая переменная, а X – независимая и постараемся найти аналитическое уравнение, математически описывающее эту зависимость. Тогда общий вид модели для каждого наблюдения исходных данных, можно записать следующим
образом:
yi =θ θ ε0 + 1xi + i , i =1,2, ,N , (9)
где N – общее число наблюдений; yi – значение признака (переменной) Y в i-м наблюдении; xi – значение признака (переменной) X в i-м наблюдении; εi – случайная величина (ошибка наблюдения); θ0 , θ1 – неизвестные параметры.
Уравнение (9) называется уравнением парной регрессии или в общем случае регрессионным уравнением. Переменные xi являются
детерминированными (неслучайными) величинами, а yi – стохастическими (случайными) величинами в силу случайности εi . Присутствие в регрессионном уравнении случайной величины εi является обязательным.
Этот факт можно объяснить целым рядом причин. Одна из них связана с тем, что наша модель является упрощением действительности, и, следовательно, в ней могут отсутствовать факторы, оказывающие влияние на отклик. Например, оборот предприятия может зависеть не только от цен на продукцию, но и от экономической ситуации в стране, действий конкурентов и ряда других факторов, которые либо не поддаются измерению, либо оказались упущены на постановочном этапе анализа. Другая причина может быть связана с наличием ошибок (погрешностей) при сборе и регистрации статистических данных.
Соотношением (9) определяется уравнение не одной прямой, а целое семейство. При этом количество возможных уравнений в семействе бесконечно и каждое уравнение из этого семейства отличается от любого другого своими значениями параметров θ0 , θ1. Таким образом, выбор «наилучшего» уравнения сводится к выбору конкретных значений
параметров θ0 и θ1.
3.2. Методы решения
Чтобы формализовать процесс выбора «наилучших» значений неизвестных параметров, необходимо ввести некоторый критерий, позволяющий однозначно определять степень отклонения модели от исходных данных. Естественно, что таких критериев может быть очень много. Приведем критерии, получившие наибольшее распространение.
1. Сумма квадратов отклонений (принцип Лежандра [ ])
N
F = ∑(yi −(θ θ0 + 1xi))2 .
i=1
Согласно этому критерию наилучшими считаются такие значения неизвестных параметров, которые соответствуют минимальному значению суммы квадратов отклонений значений зависимой переменной, рассчитанных по уравнению регрессии, от наблюдаемых значений зависимой переменной. Метод определения значений неизвестных параметров на основе
этого критерия получил название «Метод наименьших квадратов (МНК)».
К преимуществам этого метода обычно относят простоту вычислительных процедур, положенных в основу метода, а также хорошие статистические свойства получаемых оценок. Недостатками можно считать чувствительность оценок к появлению грубых ошибок в исходных данных и необходимость постулирования нормального распределения случайной
величины εi для получения некоторых дополнительных результатов. 2. Сумма модулей отклонений
N
F
=
∑![]() yi − (θ
θ0 + 1xi)
yi − (θ
θ0 + 1xi)![]() .
.
i=1
Согласно этому критерию наилучшими считаются такие значения неизвестных параметров, которые соответствуют минимальному значению суммы абсолютных величин отклонений значений зависимой переменной, рассчитанных по уравнению регрессии, от наблюдаемых значений зависимой переменной. Процесс определения значений неизвестных параметров на основе этого критерия получил название «Метод наименьших модулей
(МНМ)».
К преимуществам этого метода обычно относят значительно меньшую чувствительность результатов к появлению грубых ошибок в исходных данных, а к недостаткам – сложность вычислительных процедур, сопровождающих поиск оценок неизвестных параметров и возможность возникновения ситуаций, когда нет однозначного решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.