Модель парной линейной регрессии. Точечное и интегральное прогнозирование, страница 5

оценки θ^ˆ₀ и θ^ˆ₁, полученные по МНК, имеют наименьшую дисперсию в классе всех линейных (по y_i ) несмещенных оценок.

Доказательство теоремы можно найти в [14].

Следует обязательно отметить, что здесь речь идет только о линейных оценках. Другими словами, никто не гарантирует, что не существует нелинейной несмещенной оценки с дисперсией меньшей, чем у МНК-оценки.

То же самое можно сказать и о смещенных оценках.

3.6. Оценка дисперсии ошибки

Список неизвестных параметров модели парной регрессии не ограничивается только коэффициентами уравнения (9). Есть еще один неизвестный параметр – это дисперсия ошибок σ² . Без информации об этом параметре проведение эконометрического анализа в полном объеме становится невозможным.

На практике значение дисперсии ошибки бывает известно крайне редко, поэтому, как и в случае с коэффициентами регрессии, приходится работать с ее оценкой.

Для оценивания дисперсии ошибки нам потребуется ввести еще одно понятие – остатки модели. Под остатками модели будем понимать отклонения наблюдаемых значений отклика от предсказанных по уравнению модели (рис. 7). 

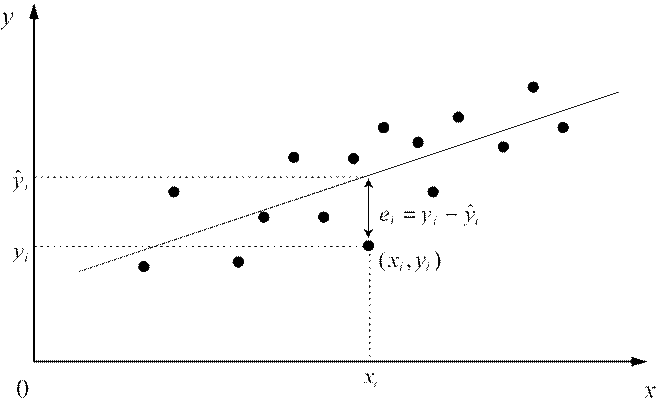
Рис. 7. Остатки уравнения регрессии

Через yˆ_i =θ θ^ˆ₀ + ^ˆ₁x_i обозначен прогноз значения y_i в точке x_i , и остатки регрессии e_i определяются из уравнения

                                                yi = yˆi + ei =θ θˆ0 + ˆ1xi + ei .

Остатки могут быть определены для каждой точки исходных данных. Однако не следует путать остатки регрессии со случайными ошибками в уравнении (9). В отличие от ошибок остатки наблюдаемы, т.е. могут быть вычислены.

Одной из особенностей процедуры метода наименьших квадратов является тот факт, что сумма остатков модели всегда нулевая

N

                                                                 ∑e_i = 0.

i=1

Остатки e_i также можно рассматривать и как оценки случайных ошибок ε_i , что позволяет их использовать при оценивании дисперсии ошибки σ² .

Рассмотрим, каким образом можно представить сумму квадратов остатков:

                                                                                                             =       y + y

∑ ∑iN=1ei2 = iN=1(yi −θ θˆ0 − ˆ1xi )2 =^yxii′′ == xyii −− xy ∑iN=1 (  i′ −θˆ0 −θˆ1x −θˆ1x′i )2=

                      N                            ₂        N                                                    ₂        N                                              2

 ∑(yi′ −θˆ1xi′) = ∑(θ ε1xi′ + i −ε−θˆ1xi′) = ∑((θ θ1 − ˆ1)xi′ +(εi −ε)) =

                    i=1                                  i=1                                                          i=1

                                   ∑N    ²( ^ˆ )2 + 2(θ θ₁ − ^ˆ₁)∑N x_i′(ε_i −ε) ⁺ ∑N (ε_i−ε)₂ .

                               ⁼    x_i′ θ θ₁ − ₁

                                     i=1                                                          i=1                             i=1

Теперь вычислим математическое ожидание каждого из полученных слагаемых.

                                         ∑N ′2(θ θ1 − ˆ1)2  = D( )θˆ1 ∑N xi′2 = Nσ2 ∑N xi′2 =σ2

                              E     xi

                                          i=1                                              i=1 ∑_xi′2 i=1

i=1

                                                     N                                    N              N                          

                     E2(θ θ1 − ˆ1)∑xi′(εi −ε) = −2E∑ ∑εjz j xi′(εi −ε) =

                                                    i=1                                   j=1          i=1                        

                                              N    N                                N               N                N

                      = −2E_∑∑x_{i i}′ε εz _{j j} −^ε∑ ∑z _jε_j x_i′_ = −2∑x z_{i i}′ σ σ² = −2 ²

                                            i= =1 j 1                          j=1             i=1          i=1

∑N (ε_i−ε)2  = E∑N ε_i2 − 2ε∑N ε_i +ε2N  =

                                       E