Модель парной линейной регрессии. Точечное и интегральное прогнозирование, страница 12

                                                              σˆ_y² = ^S     .                                                       (45) 

N

После подстановки (25) и (45) в (44) и извлечения квадратного корня получим оценку стандартной ошибки прогноза отклика в точке x_Ï

                                          σˆ_yˆÏ = .               (46) 

Из (46) видно, что значение стандартной ошибки прогноза явно зависит от точки x_Ï , в которой строится прогноз, а если говорить более точно, то от разности (x_Ï − _x). Чем больше эта разность, тем больше стандартная ошибка прогноза и ниже точность прогнозирования. Наименьшее значение

стандартной ошибки соответствует точке x_Ï = x , именно в окрестности этой точки и достигается наивысшая точность прогнозирования. Что касается доверительного интервала для y_Ï , то, как видно из (43), его ширина напрямую зависит от стандартной ошибки прогноза. На рис. 8 показано, как будут изменяться границы доверительного интервала в зависимости от прогнозной точки при фиксированном уровне доверительной вероятности (именно с этой вероятностью истинное значение отклика будет находиться в

указанных границах).

Рис. 8. Доверительный интервал уравнения регрессии

Изменение доверительной вероятности также существенно влияет на интервальный прогноз. Так, при увеличении доверительной вероятности ширина доверительного интервала должна увеличиваться, а при уменьшении – уменьшаться.

От только что рассмотренной ситуации принципиально отличается случай, когда требуется сделать прогноз при условии, что нет твердой уверенности в справедливости структуры модели. Такое возможно, если в регрессионной модели под случайной ошибкой ε подразумевается не только ошибка измерения, но и воздействие некоторых неучтенных факторов. 

Отличие состоит в том, что оценка стандартной ошибки прогноза должна вычисляться следующим образом:

                                       σˆ_yˆÏ = 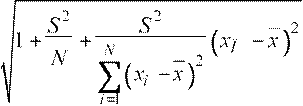 .            (47) 

Нетрудно заметить, что при расчете доверительного интервала с использованием формулы (47) вместо (46) его ширина увеличивается.

Контрольные вопросы

1.  Опишите модель парной регрессии. 

2.  Для чего в модель парной регрессии включается случайная составляющая?

3.  Перечислите известные вам методы поиска неизвестных параметров модели парной регрессии.

4.  В чем заключаются основные предположения метода наименьших квадратов?

5.  Для чего выдвигается предположение о нормальном распределении случайных ошибок?

6.  В чем разница между θ₀, θ₁ и θ^ˆ₀, θ^ˆ₁?

7.  Что показывают величины θ₀ и θ₁?

8.  Сформулируйте теорему Гаусса-Маркова.

9.  Каким образом можно оценить дисперсию случайной ошибки модели?

10. В чем разница между остатками и ошибками модели?

11. По какому закону распределены оценки параметров модели парной регрессии?

12. Что показывают величины S_θ²_ˆ0 и S_θ²_ˆ1?

13. Что такое «гипотеза о значимости параметра»? Каким образом она проверяется?

14. Чем отличается проверка значимости параметра θ₀ и параметра θ₁?

15. Как можно определить доверительный интервал для параметра регрессионного уравнения?

16. Какова зависимость ширины доверительного интервала от дисперсии случайной ошибки?

17. Что такое TSS, RSS, ESS? Как связаны между собой эти величины?

18. Как определяется и что показывает коэффициент детерминации?

19. Назовите основные свойства коэффициента детерминации.

20. Как проводится проверка значимости регрессионного уравнения?

21. Как строится таблица дисперсионного анализа?

22. Чем отличается точечное и интервальное прогнозирование?

23. В чем разница между условным и безусловным прогнозированием?

24. От чего зависит точность прогнозирования по уравнению регрессии?