Модель парной линейной регрессии. Точечное и интегральное прогнозирование, страница 4

                                        dy    (10 + 2.8 11)⋅ − (10 + 2.8 10)⋅ 40.8−38

 = = = 0.07. y (10 + 2.8 10)⋅ 38

Как видно из полученных результатов, увеличение затрат на рекламу на 10 % влечет за собой среднее увеличение оборота на 7 %.

3.5. Свойства МНК-оценок коэффициентов регрессии

Как уже отмечалось выше, оценки параметров θ^ˆ₀ и θ^ˆ₁ являются непрерывными случайными величинами, которые обладают всеми характеристиками случайных величин. Сейчас нас будут интересовать такие характеристики как математическое ожидание и дисперсия.

Нетрудно заметить, что математическое ожидание оценок параметров совпадает с истинными значениями этих параметров, т.е. МНК-оценки являются несмещенными:

                                                            ^N                                             N

∑(xi − x)( yi − y) ∑(xi − x E y) ( i − y)

                        E( )θˆ1 = ^E_ i=1 N               2       _ = i=1   N                    2            =

                                                               ∑(x_i − x)           ∑(x_i − x)

                                                                i=1                                         i=1

                                    N                                                                             N

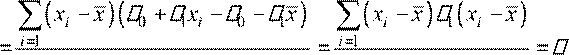                          N          1,

_N

                                                          ∑(x_i − x)²                                          ∑(x_i − x)²

                                                          i=1                                                             i=1

                E(θ^ˆ₀) = E y( − xθ^ˆ₁) = E y( ) − xE(θ θ θ θ θ^ˆ₁) = ₀ + ₁x − ₁x = ₀.

Для дальнейшего удобства изложения введем дополнительное

обозначение:

(x − x)

                                                                     zi = N      i                  ,

∑(x_i − x)²

k=1

с учетом которого можно легко записать

N

                                                          θˆ₁ = ∑z_i(y_i − y).                              (15) 

i=1

Тогда дисперсии оценок будут определяться как

                              ( )^ˆ = D∑N z_i(y_i − y) = D∑ ∑N z y_{i i}  = N z_i²σ^{2 =} _N σ2             , (16) 

                     D θ₁

                                                  i=1                             i=1           i=1                      ∑_(xi − _x)2

i=1

                                                                                                                                                                

 D(θˆ₀) = D∑N  1 − xz  y  =σ2∑N  1 − xz 2 =σ2 =

                                       i=1 N      i  i         i=1 N       i         ∑(xi − x) 

                                                                                                                                                   i=1             

N

∑xi2

                                                         =σ²        _Nⁱ⁼¹                  .                            (17) 

N∑(x_i − x)²

i=1

Как видно из этих соотношений, дисперсии оценок θ^ˆ₀ и θ^ˆ₁ зависят от дисперсии ошибки σ² , кроме этого, на точность определения параметров также оказывает влияние и расположение точек, в которых проводились измерения. 

Знание дисперсий оценок позволяет проводить их сравнение по точности – более точным оценкам соответствует меньшая дисперсия. С этой точки зрения МНК-оценки обладают рядом полезных свойств, сформулированных в виде теоремы Гаусса-Маркова [7, 14, 20].

Теорема Гаусса-Маркова. Для регрессионной модели 

                                               y_i =θ θ ε₀ + ₁x_i + _i , i =1,2,…,N ,

где для случайной ошибки выполнены условия:

                                                       E[ε_i ]= 0, i =1,2,…,N ,

                                             E D     i  1,2,…,N ,

                                                        Eεε_{i j}  = 0, i ≠ j