Модель парной линейной регрессии. Точечное и интегральное прогнозирование, страница 2

3.  Обобщенный критерий

В общем случае для решения задачи определения неизвестных параметров возможно построение других критериев:

N

                                                  F ⁼ ∑g y( _i − (θ θ₀ + ₁x_i)), 

i=1

где g u( ) – некоторая функция меры (как правило, чётная), определяющая величину отклонения значений зависимой переменной, рассчитанных по уравнению регрессии, от наблюдаемых значений зависимой переменной.

Преимущества и недостатки этого метода зависят от свойств функции меры g u( ).

Следует отметить, что на сегодняшний день наиболее широкое распространение на практике получил метод наименьших квадратов, поэтому рассмотрим его более подробно.

3.3. Оценивание параметров методом наименьших квадратов

Для того чтобы МНК приводил к получению корректных результатов, необходимо выполнение ряда предположений о случайной составляющей

уравнения (9) – ε_i .

1.  E[ε_i ]= 0, i =1,2,…,N . Это условие означает, что E y[ _i ] =θ θ₀ + ₁x_i, т.е. при фиксированном x_i среднее ожидаемое значение отклика равно θ θ₀ + ₁x_i .

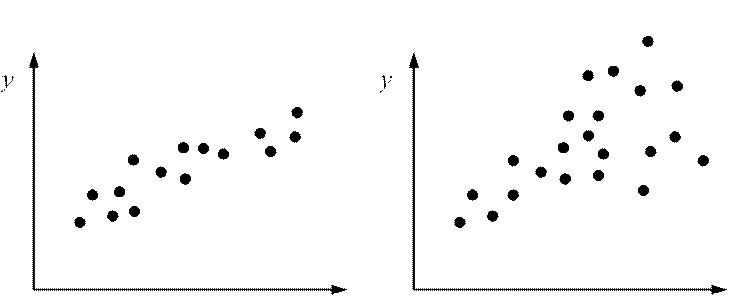
2.  E^{ }_{ }ε_i² = D[ε σ_i] = ² , i =1,2,…,N . Это условие говорит о том, что дисперсия ошибки для всех наблюдений одинакова. Это условие называется условием гомоскедастичности. Случай, когда это условие не выполняется, называется гетероскедастичностью (см. рис. 6). Также из данного условия следует, что D y[ _i]=σ², i =1,2,…,N .

       0                                           x        0                                       x

                                а                                                             б

Рис. 6. Вид исходных данных при гомоскедастичности (а) и

гетероскедастичности (б)

3.  E_εε_{i j} _ = 0, i ≠ j . Это условие указывает на некоррелированность ошибок для разных наблюдений. В случае, когда это условие не выполняется, говорят об автокорреляции ошибок.

Этих трех предположений достаточно для того, чтобы можно было использовать метод наименьших квадратов для оценивания параметров модели (9). Но если необходимо проводить более полный эконометрический анализ, то потребуется еще одно предположение – о нормальном распределении ошибок.

4.  ε_i ~ N(0,σ² ), i =1,2,…,N . При выполнении этого условия модель (9) называют нормальной линейной регрессионной моделью.

В соответствии с основной идеей метода наименьших квадратов, поиск неизвестных параметров уравнения (9) производится как решение задачи на экстремум [3]:

F =∑(yi − +(θ θ0 1xi)) → min .                                                               i=1                                                θθ0 1, Запишем необходимое условие экстремума:	(10)
 ∂F ∑N                                                          =−2    (yi − −θ θ0 1xi )= 0,                                                   ∂θ0            i=1                                                                                     .	(11)

N ²

∂F _∑N

                                                            ∂θ1 =−2i=1 xi (yi − −θ θ0 1xi )= 0.



После раскрытия скобок и приведения подобных получим систему нормальных уравнений:

                                                                                       N              N

                                                                     θ θ₀N + ₁∑ ∑x_i = y_i,

                                                                                      i=1           i=1

                                                                                           .                     (12) 

                                                                                ^ ∑ ∑ ∑N       N              2             N

                                                                   θ0      xi +θ1          xi = x yi i.

                                                                       i=1                 i=1            i=1