Разведывательный анализ данных и регрессионный анализ средствами пакета STATISTICA

Министерство образования и науки Российской Федерации

Новосибирский государственный Технический Университет

Кафедра экономической информатики

Лабораторная работа № 3

по дисциплине «Эконометрика»

на тему «Разведывательный анализ данных и регрессионный анализ средствами пакета STATISTICA»

Вариант № 2

Факультет    бизнеса

Группа:         ФБИ-41

Выполнили: Яцутко А.Ю.

                      Терпугов А.В.

Преподаватель: Наумов А.А.

Новосибирск, 2008

Цель работы:

- Получить практические навыки проведения анализа данных с использованием модулей Basic Statistics (Основные статистики), Distribution Fitting (Настройка распределения) и Multiple Regression (Множественная регрессия) пакета STATISTICA.

- Создать подробный электронный отчет о работе с описанием анализируемых данных, выполняемых статистических процедур, полученных результатов, включающий графики и таблицы. Особое  внимание уделить статистическому обоснованию выводов.

Последовательность выполнения работы

1. Подготовили исходные данные для проведения статистического анализа в системе Statistica.

1.1. Создали новую электронную таблицу для ввода данных и ввели данные.

1.2. Задали заголовок таблицы и дополнительную информацию о файле.

1.3. Задали имена переменных в соответствии с исходными данными, задали формат переменных в соответствии с их типами.

Результат  представлен на рисунке 1.

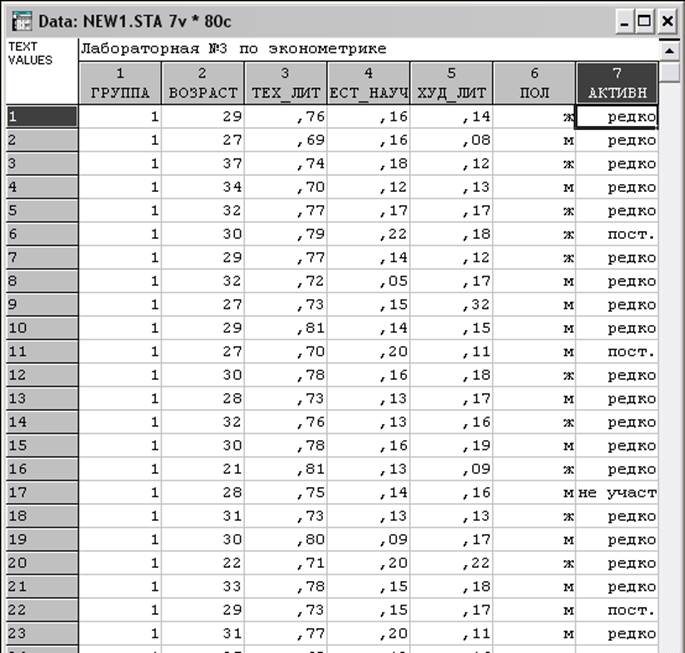
Рисунок 1. Исходные данные

2. Для выбранных данных вычислили все основные описательные статистики: математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса, медиану, верхнюю и нижнюю квартили и др. Описательные статистики для данных представлены в таблице 1. Обозначения:

Valid N - объем выборки;

Mean - среднее;

Mode - мода;

Median -медиана;

Standard Deviation - среднеквадратическое отклонение;

Variance - дисперсия;

Standard error of mean - стандартная ошибка среднего;

95% confidence limits of mean - 95 %-ный доверительный интервал для среднего;

Minimum and maximum - минимальное и максимальное значения;

Lower and upper quartiles -нижняя и верхняя квартили;

Range - размах;

Quartiles range - интерквартильный размах;

Skewness - асимметрия;

Kurtosis - эксцесс;

Standard error of skewness - стандартная ошибка асимметрии;

Standard error of kurtosis - стандартная ошибка эксцесса;

Percentile boundaries - процентили.

Таблица 1 – Описательные статистики

Descriptive Statistics (new1.sta)
			Confid.	Confid.				Lower	Upper	Quartile
	Valid N	Mean	-95,00%	95,00%	Median	Min	Max	Quartile	Quartile	Range	Variance
ВОЗРАСТ	80	27,35	26,5348	28,1652	26	21	37	25	29,5	4,5	13,42
ТЕХ_ЛИТ	80	1,0456	0,97526	1,11599	0,91	0,69	1,79	0,75	1,335	0,585	0,1
ЕСТ_НАУЧ	80	0,4025	0,34224	0,46276	0,32	0,05	0,9	0,14	0,665	0,525	0,0733
ХУД_ЛИТ	80	0,1536	0,14569	0,16156	0,16	0,08	0,32	0,125	0,17	0,045	0,0013
ПОЛ	80	100,7	100,597	100,803	101	100	101	100	101	1	0,2127
АКТИВН	80	100,58	100,448	100,702	101	100	102	100	101	1	0,3234

		Standard		Std.Err.		Std.Err.
	Std.Dev.	Error	Skewness	Skewness	Kurtosis	Kurtosis
ВОЗРАСТ	3,663366	0,409577	0,759839	0,268909	0,096085	0,531786
ТЕХ_ЛИТ	0,316203	0,035353	0,307789	0,268909	-1,46442	0,531786
ЕСТ_НАУЧ	0,270786	0,030275	0,20119	0,268909	-1,70108	0,531786
ХУД_ЛИТ	0,035658	0,003987	0,998436	0,268909	4,736905	0,531786
ПОЛ	0,461149	0,051558	-0,88964	0,268909	-1,24019	0,531786
АКТИВН	0,568698	0,063582	0,332993	0,268909	-0,80374	0,531786

Ящики с усами для исследуемых переменных представлены на рисунках 2-3.

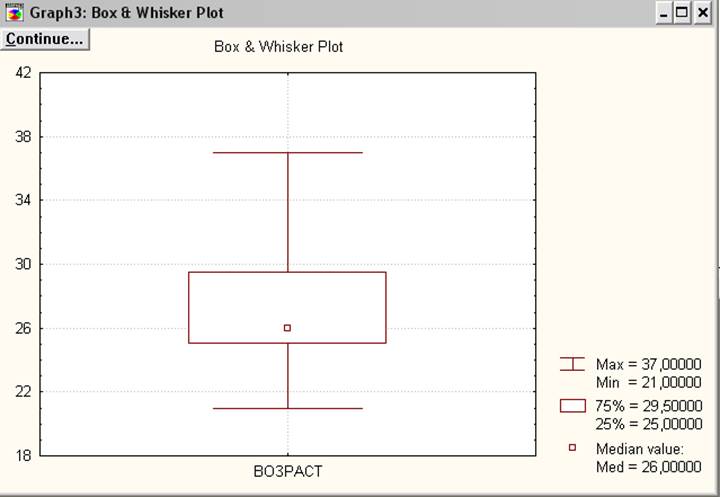
Рисунок 2. Ящик с усами

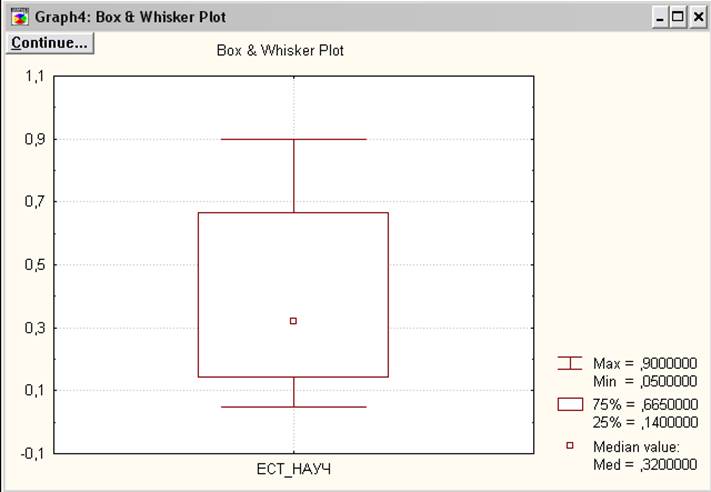
            Рисунок 3. Ящик с усами

Из рисунка 2 можно сделать вывод, что половина исследуемых людей находится в возрасте между 25 и 29,5 лет. Также мы видим среднее значение возраста людей – это 26 (минимальный возраст 21, а максимальный 37). Аналогичные выводы можно сделать по рисунку 3, где показаны значения частоты покупки литературы естественно-научного цикла через Интернет-магазин.

Для категоризованных данных ящик с усами изображен на рисунке 4.

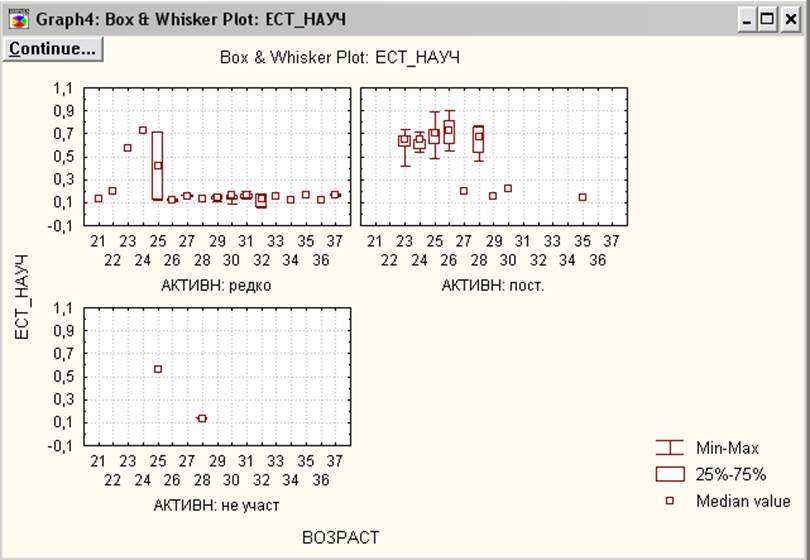
Рисунок 4. Ящик с усами

3. Для анализируемых данных строим гистограммы, таблицы частот и диаграммы типа «ствол с листьями». Гистограмма представлена на рисунке 5.

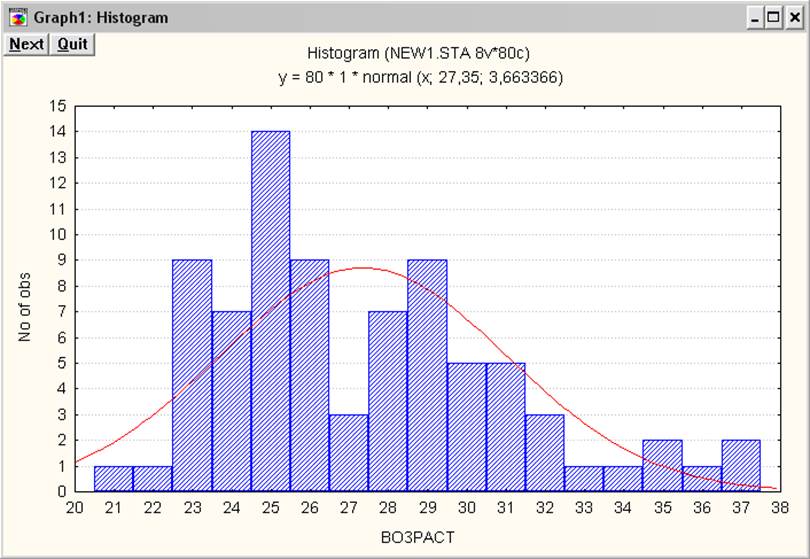
Рисунок 4. Гистограмма

Выдвигаем гипотезу о нормальном распределении показателя возраст. Таблица частот распределения представлена в таблице 2.

Таблица 2 – Частота распределения

ВОЗРАСТ (new1.sta)
		Cumul.		Cumul.
	Count	Count	Percent	Percent
21	1	1	1,25	1,25
22	1	2	1,25	2,5
23	9	11	11,25	13,75
24	7	18	8,75	22,5
25	14	32	17,5	40
26	9	41	11,25	51,25
27	3	44	3,75	55
28	7	51	8,75	63,75
29	9	60	11,25	75
30	5	65	6,25	81,25
31	5	70	6,25	87,5
32	3	73	3,75	91,25
33	1	74	1,25	92,5
34	1	75	1,25	93,75
35	2	77	2,5	96,25
36	1	78	1,25	97,5
37	2	80	2,5	100
Missing	0	80	0	100

Мы видим, что в возраст 25 лет является наиболее часто встречающимся среди посетителей Интернет-магазина, а также возраста 23, 26 и 29 ( по 11,25%). Остальные частоты являются менее значительными.

Диаграмма «Ствол с листьями» представлена на рисунке 5.

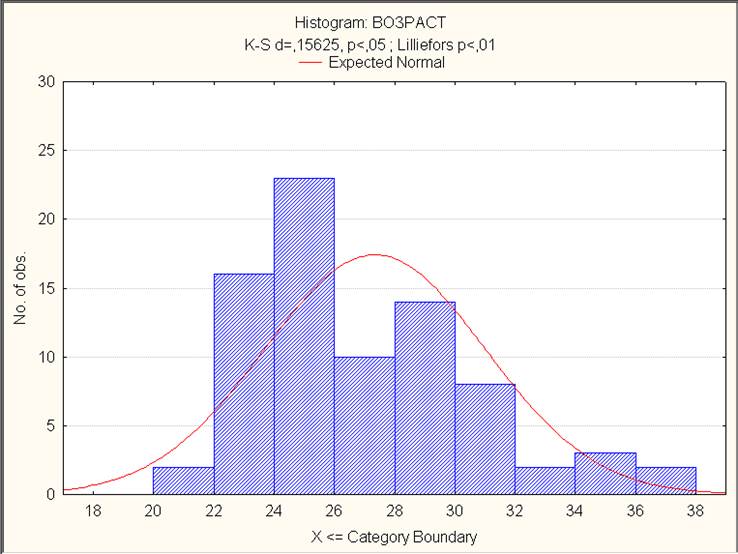
Рисунок 5. Диаграмма «Ствол с листьями»

4. С помощью критерия Пирсона и критерия Колмогорова-Смирнова проверили гипотезы о виде распределения исследуемых непрерывных и дискретных признаков, выдвинутые в п. 3. В качестве переменной взята переменная «Возраст».

На рисунке 5 изображён результат проверки гипотезы о нормальном виде распределения: