Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Отчёт
по лабораторной работе №2
Вариант 9
Группа: ФБИ-71
Студентки: Габова Л.А.
Хуторненко В.А.
Преподаватель: Колесникова А.Ю.
Новосибирск, 2011
Цель: ознакомиться с основными положениями, понятиями и методами анализа линейной модели парной регрессии.
По результатам корреляционного анализа мы выбрали пару показателей: пиво и утки, которые связаны наиболее тесно. Парный коэффициент корреляции: -0,927. Частный коэффициент корреляции: -0,758.
Обозначили их X – пиво и Y - утки.
Регрессионные уравнения:
yi=q0+qxi+ei ;
xi=q0+qyi+ei .
1. Вычислили оценки неизвестных параметров для записанных уравнений парной регрессии по методу наименьших квадратов.
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
10,279 |
,423 |
24,289 |
,000 |
|
| Пиво |
-,088 |
,007 |
-,927 |
-11,866 |
,000 |
|
a Зависимая переменная: Утки
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
107,197 |
5,286 |
20,281 |
,000 |
|
| Утки |
-9,748 |
,821 |
-,927 |
-11,866 |
,000 |
|
a Зависимая переменная: Пиво
Средний прирост количества убитых уток при единичном приросте количества выпитого пива равен -0,088. Среднее значение количества убитых уток равно 10,279 при условии, что количество выпитого пива будет равно нулю.
Средний прирост количества выпитого пива при единичном приросте количества убитых уток равен -9,748. Среднее значение количества выпитого пива равно 107,197 при условии, что количество убитых уток равно нулю.
Выбрали уравнение для дальнейшего анализа: yi=q0+qxi+ei (количество убитых уток зависят от количества выпитого пива).
2. Проверили значимость всех параметров модели по критерию Стьюдента.
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
10,279 |
,423 |
24,289 |
,000 |
|
| Пиво |
-,088 |
,007 |
-,927 |
-11,866 |
,000 |
|
a Зависимая переменная: Утки
tкрит. = 2,069 (a=0,05).
Т.о. оба параметра значимы, т.к. |tст.|>tкрит.
Т.к. оба коэффициента значимы, значит x влияет на y и константа отлична от нуля.
Построим доверительные интервалы:
q ± t кр.* Sq
9,404 < q1 < 11,154
- 0,103 < q2 < - 0,074
С вероятностью 95% коэффициенты могут принимать значения в пределах вычисленных доверительных интервалов.
3,4. Построили таблицу дисперсионного анализа, проверили значимость модели (уравнения регрессии) в целом с помощью критерия Фишера.
Дисперсионный анализ(b)
|
Модель |
Сумма квадратов |
ст.св. |
Средний квадрат |
F |
Знч. |
|
|
1 |
Регрессия |
146,680 |
1 |
146,680 |
140,801 |
,000(a) |
| Остаток |
23,960 |
23 |
1,042 |
|||
| Итого |
170,640 |
24 |
a Предикторы: (константа) Пиво
b Зависимая переменная: Утки
Fкрит. = 4,28 (a=0,05).
Т.о. модель в целом значима, т.к. Fст.>Fкрит.
Значит, эту модель можно использовать для прогнозирования.
5. Выбрали прогнозную точку: xП=100 (т.к. интервал изменения значений x от 0 до 97)
Вычислили точечную оценку yП = 1,479.
Построили 95%-ный доверительный интервал
-0,754 < yП < 3,712.
С вероятностью 95% при прогнозном количестве выпитого пива (100% от фляги) количество убитых уток будет в пределах найденного доверительного интервала.
6. Построили 95%-ный доверительный интервал для уравнения регрессии на всем диапазоне исходных данных.
|
4 |
3,36254 |
7,67083 |
|
2 |
1,02149 |
5,42638 |
|
7 |
5,54425 |
9,89827 |
|
6 |
3,9803 |
8,28764 |
|
6 |
5,19973 |
9,53732 |
|
5 |
3,80434 |
8,11086 |
|
3 |
0,47117 |
4,9185 |
|
3 |
0,83846 |
5,25668 |
|
11 |
7,15793 |
11,63553 |
|
6 |
2,11097 |
6,45329 |
|
6 |
5,63011 |
9,98877 |
|
3 |
0,56315 |
5,0029 |
|
9 |
6,22821 |
10,62523 |
|
1 |
-0,54697 |
3,99663 |
|
11 |
7,82664 |
12,37775 |
|
5 |
1,65886 |
6,02357 |
|
10 |
6,90557 |
11,35879 |
|
6 |
3,36254 |
7,67083 |
|
7 |
4,41826 |
8,7315 |
|
9 |
7,99287 |
12,56424 |
|
7 |
4,94021 |
9,26774 |
|
7 |
3,80434 |
8,11086 |
|
4 |
1,38633 |
5,767 |
|
4 |
2,38095 |
6,7124 |
|
5 |
2,11097 |
6,45329 |
7. Изобразили в одной системе координат исходные данные, линию регрессии, 95%-ный доверительный интервал.
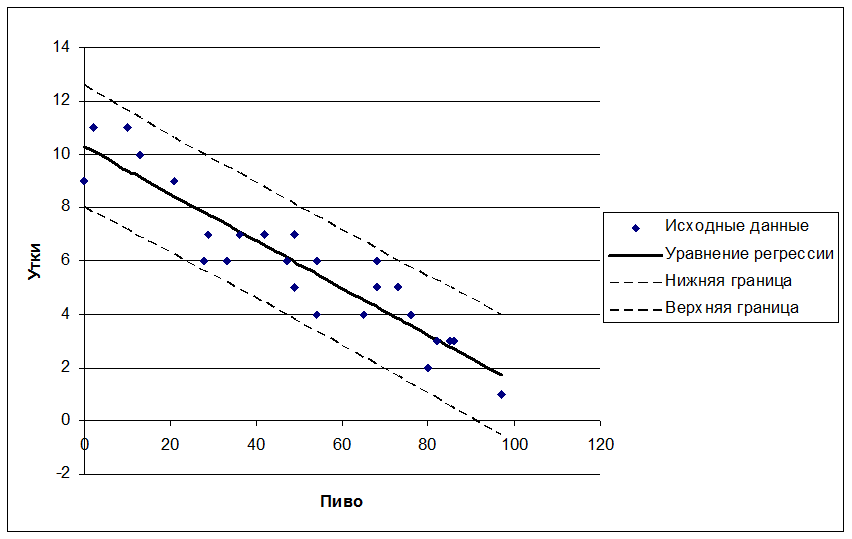
8. Общие выводы:
По результатам корреляционного анализа была выбрана пара показателей, связанных наиболее тесно – это пиво и утки. Далее из этой пары для дальнейшего анализа мы выбрали одно уравнение, в котором количество убитых уток зависит от количества выпитого пива. Далее мы вычислили оценки неизвестных параметров методом наименьших квадратов и проверили их на значимость. Значения параметров получились следующие: q0 = 10,279, q1 = -0,088. По критерию Стьюдента оба параметра оказались значимыми. При проверке значимости всей модели по критерию Фишера было выявлено, что модель в целом адекватна. Благодаря интервальному прогнозу, Робинзон теперь знает, что если он выпьет всю флягу пива, то он сможет убить всего лишь меньше четырех уток.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.