Министерство образования и науки Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра экономической информатики
Лабораторная работа №2
по дисциплине “Эконометрика”
Тема: Алгоритм Уоллиса для оценивания параметров в уравнениях с лагом
Факультет: бизнеса
Группа: ФБИ-41
Студенты: Яцутко А.Ю.
Терпугов А.В.
Преподаватель: Наумов А.А.
Новосибирск
2008
СОДЕРЖАНИЕ
Цель лабораторной работы……………………………………………………………………...3
Теоретическое описание модели………………………………………………………………..3
Код программы…………………………………………………………………………………..4
Результаты работы программы…………………………………………………………………7
Выводы………………………………………………………………………………………….21
Список литературы……………………………………………………………………………..22
Цель лабораторной работы:
1) Реализовать с помощью Matlab алгоритм Уоллиса и определить его эффективность для оценки параметров в уравнениях с лагом
2) Проверить справедливость вывода Уоллиса о меньшей смущенности его оценки по сравнению с оценкой, получаемой с помощью инструментальной переменной
Теоретическое описание модели:
Метод оценивания, предложенный Уоллисом, состоит из трёх этапов:
![]() , (1)
, (1)
где Xt-1 используется в качестве инструментальной переменной для Yt-1. Таким образом, оценку векторов регрессии можно вычислить по формуле 2
![]() , (2)
, (2)
где
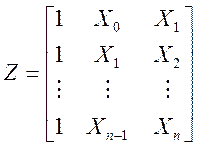 (3)
(3)
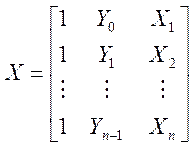 (4)
(4)
Автокорреляция – корреляционная зависимость между последовательными элементами ряда.
Свойства коэффициента автокорреляции:
1. Он строится по аналогии с линейным коэффициентом корреляции и характеризует тесноту только линейной связи текущего и предыдущего уровней ряда.
2. По знаку коэффициента автокорреляции нельзя сделать вывод о возрастающей или убывающей тенденции в уровнях ряда
Для остатков регрессии, вычисляемых по формуле 5, рассчитывается коэффициент автокорреляции первого порядка с учетом поправки на смещение по формуле 6:
![]() (5)
(5)
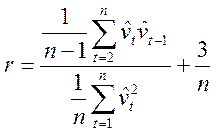 . (6)
. (6)
С помощью полученной оценки для r получают матрицу ![]() , которая рассчитывается по формуле 7:
, которая рассчитывается по формуле 7:
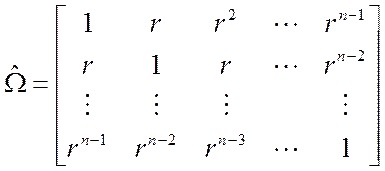 (7)
(7)
и рассчитывают оценку вектора ![]() обобщенным
методом наименьших квадратов (формула 8)
обобщенным
методом наименьших квадратов (формула 8)
![]() (8)
(8)
ПРОГРАММА
В программе используется функция ModelM (bn, Y, X, sigma) возвращающая значение уравнения с лагом вида:
![]()
Описание параметров функции ModelM:
bn=[ ![]() ,
, ![]() ,
, ![]() ] – вектор коэффициентов
] – вектор коэффициентов
Y –
вектор ![]()
X –
вектор ![]()
Sigma – Значение σ, константа, задается в теле программы
Код программы:
Главный модуль программы:
function [ x ] = mainM()
% Задаем исходные дынные
%-------------------------------
Y0=0.5;
sigma=1.5;
step = 0.01;
n=28
X0=0.5;
bn=[0.5 1 1.5]';
T=100
kolvo_vector=[]
%-------------------------------
%for n = 1: T
%kolvo=0;
X = [1:n]';
S=cycle(Y0,sigma,step,n,X,bn,X0);% Ищем решение
graphik(step,sigma,S(1,:),S(2,:));% Строим график
%for n = 1: length (S(1,:)-S(2,:))
%if (S(2,n)-S(1,n))<0
% kolvo=kolvo+1
%end
%end
%kolvo_vector=[kolvo_vector kolvo]
%end
%plot(X',kolvo_vector)
Модуль поиска решения:
function [ x1 ] = cycle(Y0,sigma,step,n,X,bn,X0)
beta_vector=[]
b_vector=[]
Z=[1 X0 X(1)];
for i= 2 : n
Z(i, 1) = 1;
Z(i, 2) = X (i-1);
Z(i, 3) = X (i);
end
Z; % Formed Z
y = 1;
XGraph = [0.01:step:sigma]';
for sx = 0.01: step: sigma
% That means X=1 Yo X1
XF=[1 Y0 X(1)];
% 1
Y(1)= ModelM (bn, Y0, X(1), sigma);
for i= 2 : n
Y(i,1)= ModelM (bn, Y(i-1), X(i), sigma);
XF(i,1:3)=[1 Y(i-1) X(i)];
end
Z;
XF;
beta = inv(Z'*XF)*Z'*Y;
%%%%%% 2 punkt - poluchenie coefficienta autocorrelacii
veta = Y - XF*beta;
sum1 = 0;
sum2 = 0;
for t = 2: n
sum1=sum1+(veta(t)*veta(t-1))/(n-1);
end
for t = 1: n
sum2 = sum2 + (veta(t)^2)/n;
end
r = sum1/sum2 + 3/n;
r;
%%%%%% 3 punkt - poluchenie matricy ocenki
for i = 1: n
for j = 1: n
omega(i,j) = r^(abs(i-j));
end
end
omega;
b = inv(XF'*inv(omega)*XF)*XF'*inv(omega)*Y;
beta_vector=[beta_vector beta];
b_vector=[b_vector b];
sum_beta(y) = (bn-beta)'*(bn-beta);
sum_b(y) = (bn-b)'*(bn-b);
y = y+1;
end %sigma
x1 =[sum_b;sum_beta];
plot(XGraph,beta_vector);
pause;
plot(XGraph,b_vector);
pause;
Модуль поиска
значения функции вида ![]() :
:
% Model for Test
function [ f ] = ModelM( bn, Y, X, sigma )
f = bn(1) + bn(2)*Y + bn(3)*X + randn*sigma;
Модуль вывода найденного решения на экран:
function [ output_args ] = graphik(step,sigma,sum_b,sum_beta )
XGraph = [0.01:step:sigma]';
sum_b;
sum_beta;
% Building graph
plot(XGraph,sum_b,XGraph,sum_beta)
pause
plot(XGraph,(sum_beta-sum_b))
Результаты работы программы:
На рисунке 1 представлена диаграмма, отражающая значения коэффициентов бета на каждой из итераций полученных методом оценки с использованием инструментальной переменной.
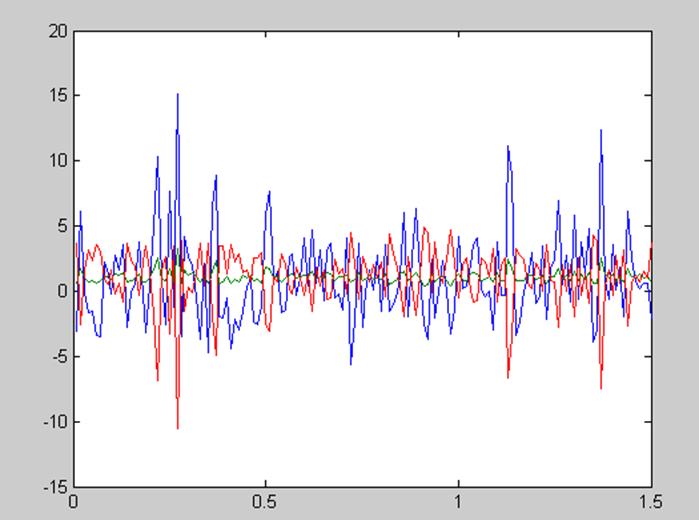
Рисунок 1. – Диаграмма, отражающая значения коэффициентов бета на каждой из итераций, полученных методом оценки с использованием инструментальной переменной при количестве периодов равном 7.
На рисунке 2 представлена диаграмма, отражающая значения коэффициентов бета на каждой из итераций полученных методом оценки Уоллиса.
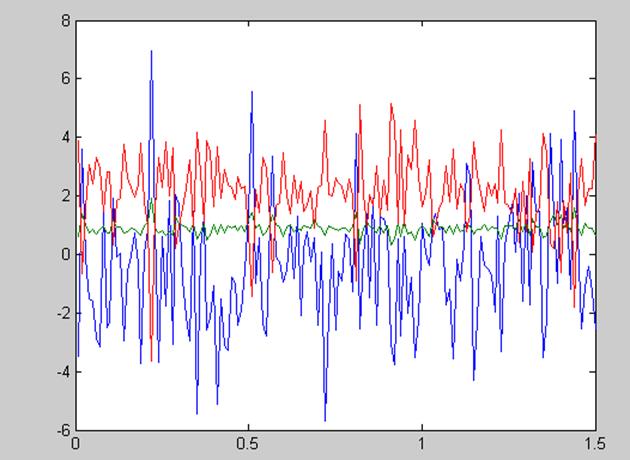
Рисунок 2. – Диаграмма, отражающая значения коэффициентов бета на каждой из итераций, полученных методом оценки Уоллиса при количестве периодов равном 7.
В результате выполнения функции Graphik на экран была выведена диаграмма, изображенная на рисунке 3.
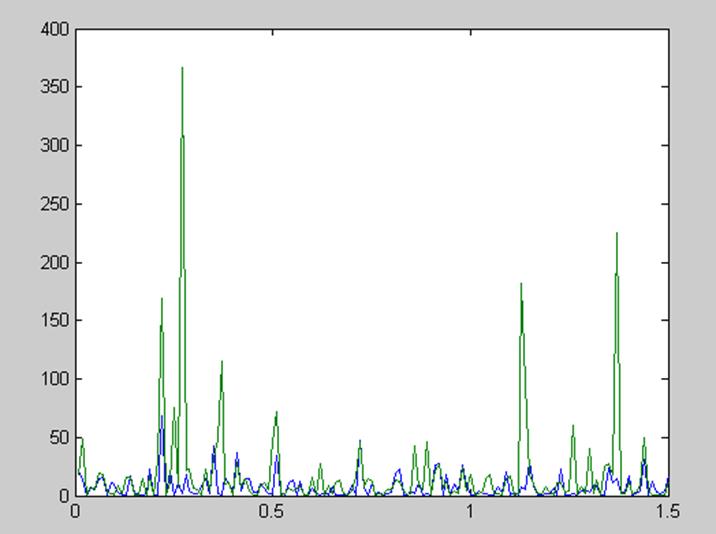
Рисунок 3. – Сравнение решения задачи c использованием инструментальной переменной с решением по алгоритму Уоллиса при количестве периодов равном 7
По горизонтальной оси отложен доверительный интервал s = [0:1.5]. Эксперимент проводился с шагом сигма = 0,01. Прямой зависимости отклонений от роста сигма не замечено, это может говорить об устойчивости обоих алгоритмов к шумам. Также четко видно, что оценка, полученная на 3м шаге алгоритма Уоллиса существенно точнее оценки, полученной на первом шаге. Этот факт ярче отражен на второй диаграмме, которая изображена на рисунке 4.
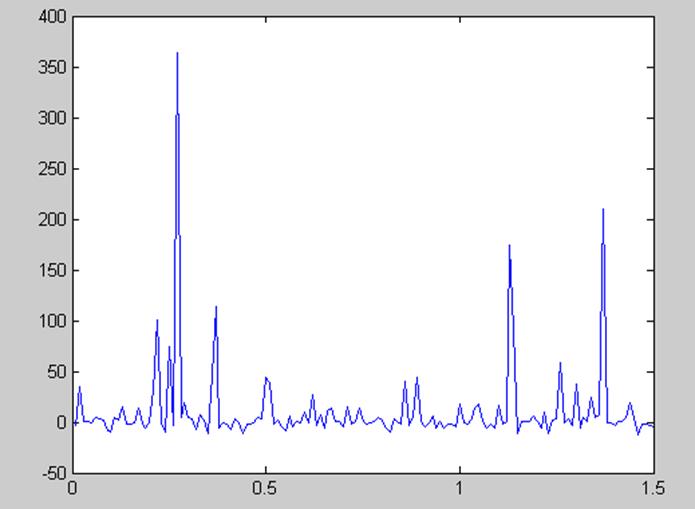
Рисунок 4. – Разница графика, полученного на первом шаге и на третьем шаге алгоритма Уоллиса с периодом равным 7
На этом графике показана разность квадратов отклонений оценки алгоритмом Уоллиса на первом шаге и на третьем шаге. Очевидно, что большая часть графика лежит в положительной части оси ординат, что свидетельствует о повышении точности оценки на 3м шаге.
Если увеличить число периодов с 7ми до 28ми, то получим диаграмму, изображенную на рисунках 5,6,7,8.
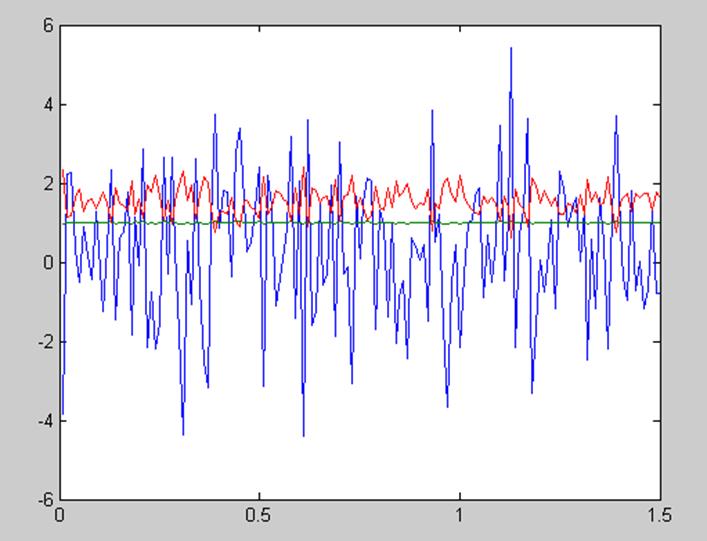
Рисунок 5. – Диаграмма, отражающая значения коэффициентов бета на каждой из итераций, полученных методом оценки с использованием инструментальной переменной при количестве периодов равном 28.
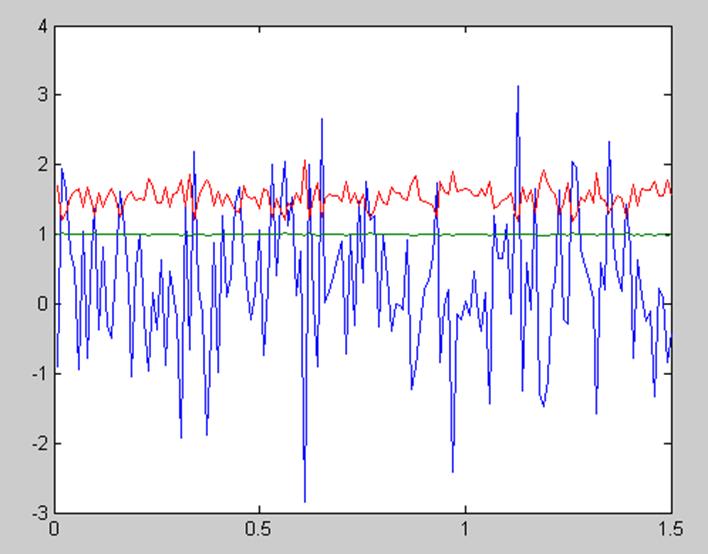
Рисунок 6. – Диаграмма, отражающая значения коэффициентов бета на каждой из итераций, полученных методом оценки с использованием инструментальной переменной при количестве периодов равном 28.
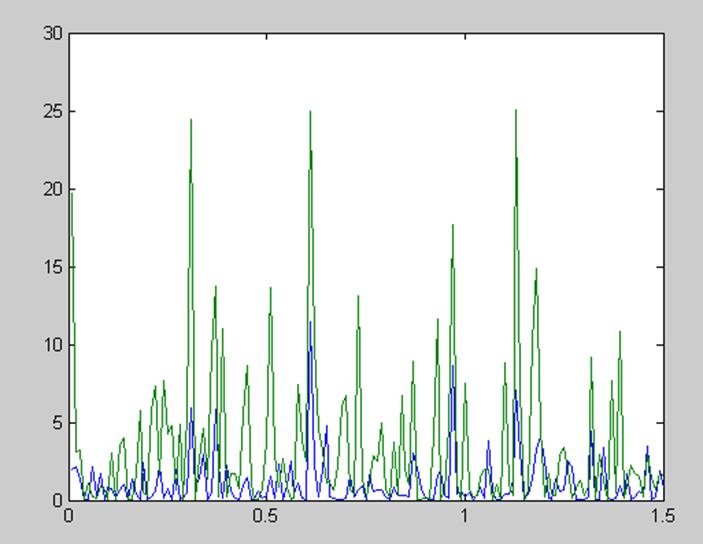
Рисунок 7. – Сравнение решения задачи c использованием инструментальной переменной с решением по алгоритму Уоллиса при количестве периодов равном 28
По графику видно, что точность обеих оценок существенно выросла. Теперь посмотрим, какая оценка становится точнее при увеличении числа наблюдений. Разница графика, полученного на первом шаге и на третьем шаге алгоритма Уоллиса с периодом равным 21 изображена на рисунке 8.
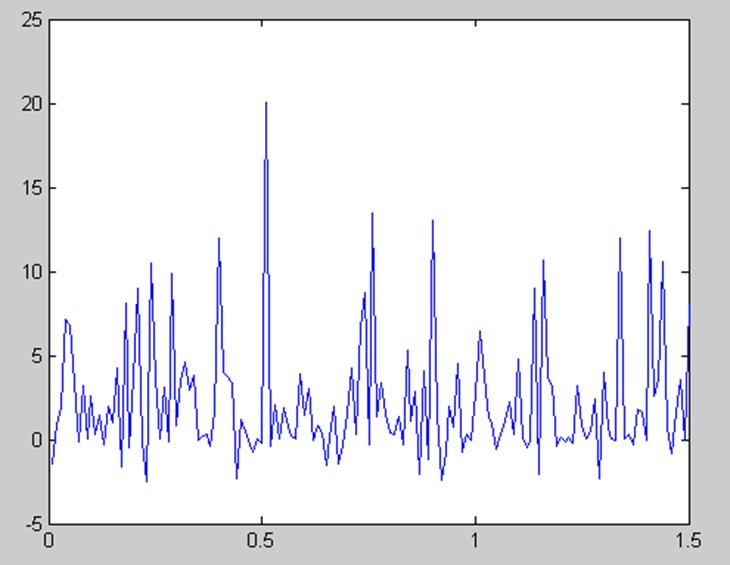
Рисунок 8. – Разница графика, полученного на первом шаге и на третьем шаге алгоритма Уоллиса с периодом равным 21
Очевидно, что точность алгоритма Уоллиса на 3м шаге увеличилась больше, чем его точность на 1м шаге. Теперь практически нет точек в отрицательной части оси ординат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.