Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Отчёт
по лабораторной работе №3
Вариант 9
Группа: ФБИ-71
Студентки: Габова Л.А.
Хуторненко В.А.
Преподаватель: Колесникова А.Ю.
Новосибирск, 2011
Цель: ознакомиться с основными положениями, понятиями и методами анализа линейных моделей множественной регрессии.
Ход работы:
1. Уравнение зависимости веса собранного урожая от количества обобранных кустов винограда и орешника:
![]()
где ![]() -
вес
собранного урожая, фунты;
-
вес
собранного урожая, фунты;
![]() ,
, ![]() ,
, ![]() -
неизвестные
параметры;
-
неизвестные
параметры;
![]() - количество
обобранных кустов винограда, шт.;
- количество
обобранных кустов винограда, шт.;
![]() - количество
обобранных кустов орешника, шт.;
- количество
обобранных кустов орешника, шт.;
![]() - случайная
компонента, ошибка наблюдения.
- случайная
компонента, ошибка наблюдения.
2. С помощью метода наименьших квадратов нашли оценки всех неизвестных параметров уравнения регрессии.
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
,980 |
4,940 |
,198 |
,845 |
|
| Виноград |
1,152 |
,327 |
,424 |
3,528 |
,002 |
|
| Орехи |
3,164 |
,620 |
,613 |
5,101 |
,000 |
|
a Зависимая переменная: Вес
Средний прирост веса собранного урожая при единичном приросте количества обобранных кустов винограда составляет 1,152 фунта.
Средний прирост веса собранного урожая при единичном приросте количества обобранных кустов орешника составляет 3,164 фунта.
Среднее значение веса собранного урожая при условии, что количество обобранных кустов винограда и орешника равно нулю, составляет 0,98 фунтов (вес корзины).
3. Проверили значимость параметров уравнения по критерию Стьюдента
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
,980 |
4,940 |
,198 |
,845 |
|
| Виноград |
1,152 |
,327 |
,424 |
3,528 |
,002 |
|
| Орехи |
3,164 |
,620 |
,613 |
5,101 |
,000 |
|
a Зависимая переменная: Вес
tкрит. = 2,069 (a=0,05).
Т.о. параметры ![]() и
и ![]() значимы,
т.к. |tст.|>tкрит.,
а параметр
значимы,
т.к. |tст.|>tкрит.,
а параметр ![]() не значим, т.к. |tст.|<
tкрит.
не значим, т.к. |tст.|<
tкрит.
Так как коэффициенты значимы, значит xi влияет на y, а константой можно пренебречь, потому что она не значима.
Построим доверительные интервалы для значимых параметров:
q ± t кр.* Sq
0.475 < q1 < 1.829
1.881 < q2 < 4.447
С вероятностью 95% коэффициенты могут принимать значения в пределах вычисленных доверительных интервалов.
Рассчитали коэффициенты эластичности:
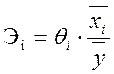
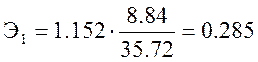
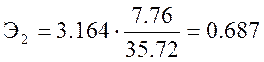
При изменении количества обобранных кустов винограда на 1% вес собранного урожая изменится на 28,5%.
При изменении количества обобранных кустов орешника на 1% вес собранного урожая изменится на 68,7%.
4. Вычислили коэффициент детерминации и проверили на значимость построенное регрессионное уравнение.
Дисперсионный анализ(b)
|
Модель |
Сумма квадратов |
ст.св. |
Средний квадрат |
F |
Знч. |
|
|
1 |
Регрессия |
1483,935 |
2 |
741,968 |
26,887 |
,000(a) |
| Остаток |
607,105 |
22 |
27,596 |
|||
| Итого |
2091,040 |
24 |
a Предикторы: (константа) Орехи, Виноград
b Зависимая переменная: Вес
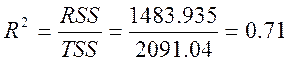
Сводка для модели
|
Модель |
R |
R квадрат |
Скорректированный R квадрат |
Стд. ошибка оценки |
|
1 |
,842(a) |
,710 |
,683 |
5,25316 |
a Предикторы: (константа) Орехи, Виноград
Коэффициент детерминации показывает долю объясненной дисперсии. Коэффициент детерминации близок к 1, значит уравнение регрессии достаточно точно описывает данные.
Fкрит. = 3,4221.
Т.о. модель в целом значима, т.к. Fст.>Fкрит.
Значит, эту модель можно использовать для прогнозирования.
Сделали проверку на мультиколлинеарность.
1) Изменили исходные данные путем изъятия малого количества наблюдений и оценили неизвестные параметры.
Коэффициенты(a)
|
Модель |
Нестандартизованные коэффициенты |
Стандартизованные коэффициенты |
t |
Знч. |
||
| B |
Стд. ошибка |
Бета |
||||
| 1 |
(Константа) |
2,614 |
4,836 |
,541 |
,595 |
|
| Виноград |
1,311 |
,329 |
,505 |
3,986 |
,001 |
|
| Орехи |
2,705 |
,631 |
,543 |
4,286 |
,000 |
|
a Зависимая переменная: Вес
Оценки значимых параметров изменились незначительно, значит этот признак мультиколлиниарности отсутствует.
2) Все оценки параметров имеют логичные знаки и величины с экономической точки зрения, значит этот признак отсутствует.
3) У всех значимых оценок коэффициентов регрессии имеются небольшие стандартные ошибки и большую значимость, в то время, как всё уравнение в целом значимо (большое значение коэффициента детерминации). Значит этот признак мультиколлинеарности отсутствует.
Так как все три признака не выполняются, значит мультиколлинеарность отсутствует.
5. Построили 95%-ый доверительный интервал для уравнения регрессии на всём диапазоне исходных данных.
|
вес |
нижн.гр. |
верхн.гр. |
|
44 |
28,60778 |
51,04788 |
|
49 |
34,93266 |
58,55139 |
|
23 |
25,54589 |
48,36766 |
|
34 |
31,52166 |
54,46216 |
|
45 |
26,68038 |
48,95186 |
|
25 |
12,06495 |
35,36392 |
|
45 |
32,69788 |
55,59067 |
|
32 |
15,49031 |
38,26671 |
|
16 |
9,58099 |
33,23842 |
|
48 |
35,98733 |
59,21541 |
|
31 |
17,50358 |
40,27686 |
|
33 |
23,10156 |
46,78856 |
|
36 |
24,37775 |
46,64503 |
|
36 |
30,30564 |
53,37345 |
|
29 |
22,24164 |
45,89038 |
|
29 |
16,56351 |
40,08427 |
|
41 |
26,53512 |
49,68316 |
|
34 |
23,16479 |
45,55327 |
|
29 |
16,19458 |
39,28113 |
|
32 |
16,56351 |
40,08427 |
|
22 |
11,63486 |
35,20797 |
|
48 |
35,98733 |
59,21541 |
|
38 |
29,82956 |
52,71687 |
|
43 |
26,17819 |
48,86801 |
|
51 |
31,52166 |
54,46216 |
6. Изобразили в одной системе координат исходные данные, линию регрессии, 95%-ный доверительный интервал.
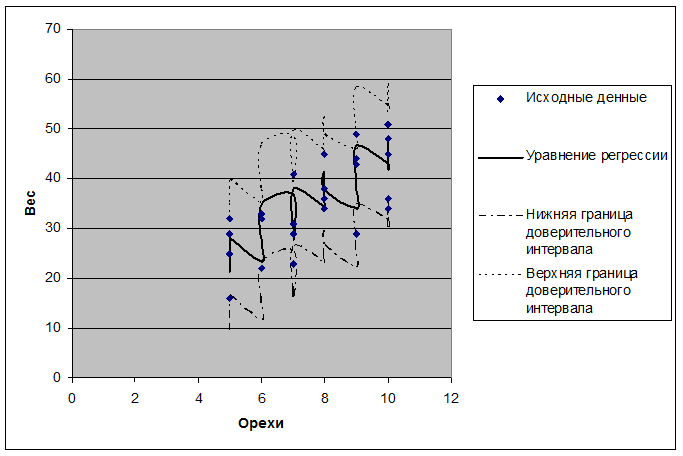
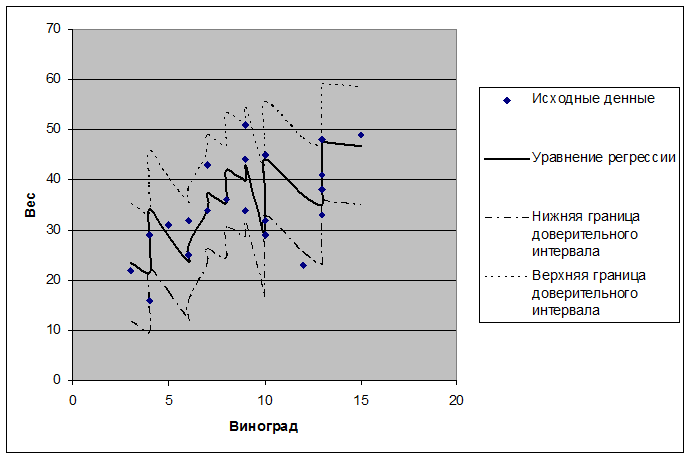
7. Общие выводы: уравнение зависимости веса собранного урожая от
количества обобранных кустов винограда и орешника выглядит следующим образом:
![]()
Значением константы мы пренебрегли, так как её значение по критерию Стьюдента не значимо для модели. В целом, модель значима и адекватна по критерию Фишера, следовательно, её можно использовать для дальнейшего анализа и прогнозирования.
Расчет коэффициентов эластичности показал, что если Робинзон будет обирать кусты винограда на 1% больше, то вес собранного урожая изменится на 28,5%, а при увеличении обобранных кустов орешника на 1% вес собранного урожая изменится на 68,7%.
МУЛЬТИКОЛЛИНЕАРНОСТЬ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.