Экономика и менеджмент \ Эконометрика

Алгоритм Уоллиса для оценивания параметров в уравнениях с лагом, страница 2

Далее доработаем программу и проверим, как влияет количество интервалов на соотношение точности алгоритма Уоллиса на 1 и 3 шаге. На рисунке 9 отражена зависимость количества точек в отрицательных части оси координат графика, отражающего разность оценок на первом и третьем шагах.

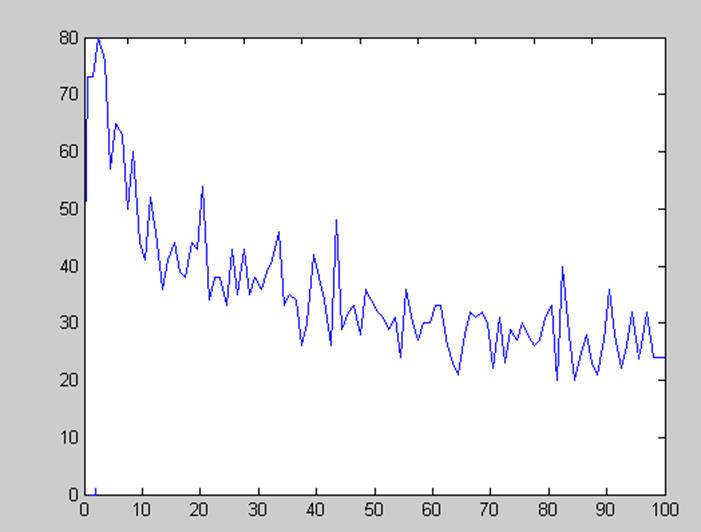
Рисунок 9. – Зависимость количества точек в отрицательных части оси координат графика, отражающего разность оценок на первом и третьем шагах

Невооруженным глазом видно, что количество точек с ростом периодов уменьшается по экспоненте.


РЕАЛЬНЫЙ ПРИМЕР

Вектор X – Вложения в ценные бумаги; Y – прибыль.

Прибыль

Вложения в рекламу

140

40

145

41

147

41.6

152

42

160

46

161

46.6

163

47

162

45

152

43

138

41

140

41.5

141

42.2

143

43.3

144

44

148

44.2

149

42

151

41

151.3

39

151.5

38

151.8

37.4

152

37.2

152.2

36.5

152.6

36

153

35.5

Текст программы под реальные данные.

Файл  cycle:

function [ x1 ] = cycle(Y0,sigma,step,n,X,bn1,bn2,bn3,bn4,X0)

beta_vector=[]

b_vector=[]

kolvo=0

y_vector=[]

Z3=[

1 41 41.5

1 41.5 42.2

1 42.2 43.3

1 43.3 44

1 44 44.2

]

Z4=[

1 44.2 42

1 42 41

1 41 39

1 39 38

1 38 37.4

1 37.4 37.2

1 37.2 36.5

1 36.5 36

1 36 35.5

]

Z2=[

1 47 45

1 45 43

1 43 41

 ]

Z1=[   

1 39 40

1 40 41

1 41 41.6

1 41.6 42

1 42 46

1 46 46.6

1 46.6 47

]

XF1=[

1 140 40

1 145 41

1 147 41.6

1 152 42

1 160 46

1 161 46.6

1 163 47

]

XF2=[

1 162 45

1 152 43

1 138 41

]

XF3=[

1 140 41.5

1 141 42.2

1 143 43.3

1 144 44

1 148 44.2

]

XF4=[

1 149 42

1 151 41

1 151.3 39

1 151.5 38

1 151.8 37.4

1 152 37.2

1 152.2 36.5

1 152.6 36

1 153 35.5

]

%Z=[1 X0 X(1)];

%for i= 2 : n

%    Z(i, 1) = 1;

%    Z(i, 2) = X (i-1);

%    Z(i, 3) = X (i);

%end   

%Z; % Formed Z

y = 1;

%------------------Тестируем предположение---------------------------

%7 3 10 4

Y1(1)= ModelM (bn1, Y0, X(1), sigma);

%y_vector=Y(1);

for m= 2 : 7

    Y1(m,1)= ModelM (bn1, Y1(m-1), X(m), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

beta = inv(Z1'*XF1)*Z1'*Y1;

veta = Y1 - XF1*beta;

sum1 = 0;

sum2 = 0;

for t = 2: 7

   sum1=sum1+(veta(t)*veta(t-1))/(7-1);

end

for t = 1: 7

   sum2 = sum2 + (veta(t)^2)/7;

end

r = sum1/sum2 + 3/7;

r;

%%%%%% 3 punkt - poluchenie matricy ocenki

for i = 1: 7

   for j = 1: 7

      omega(i,j) = r^(abs(i-j));

   end

end

omega;

b = inv(XF1'*inv(omega)*XF1)*XF1'*inv(omega)*Y1;

Y1(1)= ModelM (b, Y0, X(1), sigma);

for m= 2 : 7

    Y1(m,1)= ModelM (b, Y1(m-1), X(m), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

%plot([1:7]',Y1,'b.:',[1:7]',XF1(:,2),'sr-');

%----------------------------------------------

Y2(1)= ModelM (bn2, Y1(7), X(8), sigma);

%y_vector=Y(1);

for m= 2 : 3

    Y2(m,1)= ModelM (bn2, Y2(m-1), X(m+7), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

beta = inv(Z2'*XF2)*Z2'*Y2;

veta = Y2 - XF2*beta;

sum1 = 0;

sum2 = 0;

for t = 2: 3

   sum1=sum1+(veta(t)*veta(t-1))/(3-1);

end

for t = 1: 3

   sum2 = sum2 + (veta(t)^2)/3;

end

r = sum1/sum2 + 3/3;

r;

%%%%%% 3 punkt - poluchenie matricy ocenki

omega=[];

for i = 1: 3

   for j = 1: 3

      omega(i,j) = r^(abs(i-j));

   end

end

omega;

b = inv(XF2'*inv(omega)*XF2)*XF2'*inv(omega)*Y2;

Y2(1)= ModelM (b, Y1(7), X(8), sigma);

for m= 2 : 3

    Y2(m,1)= ModelM (b, Y2(m-1), X(m+7), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

%plot([1:3]',Y2,'b.:',[1:3]',XF2(:,2),'sr-');

%----------------------------------------------

Y3(1)= ModelM (bn3, Y2(3), X(11), sigma);

%y_vector=Y(1);

for m= 2 : 5

    Y3(m,1)= ModelM (bn3, Y3(m-1), X(m+10), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

beta = inv(Z3'*XF3)*Z3'*Y3;

veta = Y3 - XF3*beta;

sum1 = 0;

sum2 = 0;

for t = 2: 5

   sum1=sum1+(veta(t)*veta(t-1))/(55-1);

end

for t = 1: 5

   sum2 = sum2 + (veta(t)^2)/5;

end

r = sum1/sum2 + 3/5;

r;

%%%%%% 3 punkt - poluchenie matricy ocenki

omega=[];

for i = 1: 5

   for j = 1: 5

      omega(i,j) = r^(abs(i-j));

   end

end

omega;

b = inv(XF3'*inv(omega)*XF3)*XF3'*inv(omega)*Y3;

Y3(1)= ModelM (b, Y2(3), X(11), sigma);

for m= 2 : 5

    Y3(m,1)= ModelM (b, Y3(m-1), X(m+10), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

%----------------------------------------------------------

Y4(1)= ModelM (bn4, Y3(5), X(16), sigma);

%y_vector=Y(1);

for m= 2 : 9

    Y4(m,1)= ModelM (bn4, Y4(m-1), X(m+15), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

beta = inv(Z4'*XF4)*Z4'*Y4;

veta = Y4 - XF4*beta;

sum1 = 0;

sum2 = 0;

for t = 2: 9

   sum1=sum1+(veta(t)*veta(t-1))/(9-1);

end

for t = 1: 9

   sum2 = sum2 + (veta(t)^2)/9;

end

r = sum1/sum2 + 3/9;

r;

%%%%%% 3 punkt - poluchenie matricy ocenki

omega=[];

for i = 1: 9

   for j = 1: 9

      omega(i,j) = r^(abs(i-j));

   end

end

omega;

b = inv(XF4'*inv(omega)*XF4)*XF4'*inv(omega)*Y4;

Y4(1)= ModelM (b, Y3(3), X(16), sigma);

for m= 2 : 9

    Y4(m,1)= ModelM (b, Y4(m-1), X(m+15), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

end

%-------------------------------------------------------

%plot([1:14]',Y3,'b.:',[1:14]',XF3(:,2),'sr-');

plot([1:24]',[Y1; Y2; Y3;Y4]','b.:',[1:24]',[XF1(:,2); XF2(:,2); XF3(:,2); XF4(:,2)],'sr-');

pause;

%------------------Тестируем предположение------------------------------

%XGraph = [0.01:step:sigma]';

%for sx = 0.01: step: sigma

% That means X=1 Yo X1

%XF=[1 Y0 X(1)];

%b=[1 2 3]

% 1

%m=0;

%Y(1)= ModelM (bn, Y0, X(1), sigma);

%y_vector=Y(1);

%for m= 2 : n

%    Y(m,1)= ModelM (bn, Y(m-1), X(m), sigma);

%   XF(i,1:3)=[1 Y(i-1) X(i)];

%end

%Z;

%XF;

%beta = inv(Z'*XF)*Z'*Y;

%%%%%% 2 punkt - poluchenie coefficienta autocorrelacii

%veta = Y - XF*beta;

%sum1 = 0;

%sum2 = 0;

%for t = 2: n

%   sum1=sum1+(veta(t)*veta(t-1))/(n-1);

%end

%for t = 1: n

%   sum2 = sum2 + (veta(t)^2)/n;

%end

%r = sum1/sum2 + 3/n;

%r;

%%%%%% 3 punkt - poluchenie matricy ocenki

%for i = 1: n

%   for j = 1: n

%%      omega(i,j) = r^(abs(i-j));

%   end

%end

%omega;

%b = inv(XF'*inv(omega)*XF)*XF'*inv(omega)*Y;

%beta_vector=[beta_vector beta];

%b_vector=[b_vector b];

%sum_beta(y) = (bn-beta)'*(bn-beta);

%sum_b(y) = (bn-b)'*(bn-b);

%y = y+1;

%end %sigma

%x1 =[sum_b;sum_beta];

%plot(XGraph,beta_vector);

%pause;

%plot(XGraph,b_vector);

%pause;

%pause;

%TIME = ;

%plot([1:n]',Y,'b.:',[1:n]',XF(:,2),'sr-');

end   

%pause

Файл main:

function [ x ] = mainM()

% Задаем исходные дынные

%-------------------------------

Y0=139;

sigma=0.25;

step = 0.01;

n=24   

X0=39.000;

X=[

40

41

41.6

42

46

46.6

47

45

43

41

41.5

42.2

43.3

44

44.2

42

41

39

38

37.4

37.2

36.5

36

35.5

];

T=24

kolvo_vector=[]

%-------------------------------

%for n = 1: T

bn1=[0.0001 1 0.1021]';

bn2=[0.0001 1 -0.165]';

bn3=[0.0001 1 0.045]';

bn4=[0.0001 1 0.02]';

%kolvo=0;

%X = [1:n]';

S=cycle(Y0,sigma,step,n,X,bn1,bn2,bn3,bn4,X0);% Ищем решение

%graphik(step,sigma,S(1,:),S(2,:));% Строим график

%for n = 1: length (S(1,:)-S(2,:))

%if (S(2,n)-S(1,n))<0

%    kolvo=kolvo+1

%end

%end

%kolvo_vector=[kolvo_vector kolvo]

%end

%plot(X',kolvo_vector)

Файл graphik:

function [ output_args ] = graphik(step,sigma,sum_b,sum_beta )

XGraph = [0.01:step:sigma]';

sum_b;

sum_beta;

%Building graph

plot(XGraph,sum_b,XGraph,sum_beta)

%pause

plot(XGraph,(sum_beta-sum_b))

pause

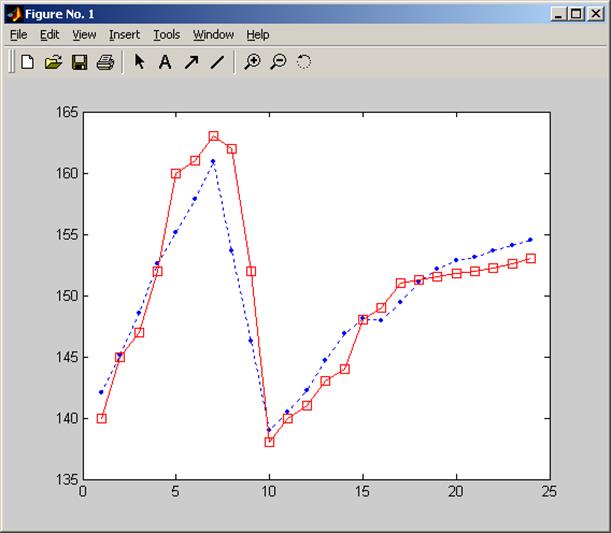
Выводы: в ходе проделанной работы мы реализовали алгоритм Уоллиса в среде Matlab и оценили с его помощью параметров уравнения с лагом. Также мы на практике убедились в справедливости вывода Уоллиса о меньшей смещенности его оценки по сравнению с оценкой, получаемой с помощью инструментальной переменной.

Список литературы:

  1. Джонстон Дж. Эконометрические методы./ Пер. с англ. – М.: Статистика, 1980.
Скачать файл