Разведывательный анализ данных и регрессионный анализ средствами пакета STATISTICA, страница 4

В рассматриваемом примере толерантность для всех переменных довольно высокая. Наименьшее значение толерантности имеет переменная x6, однако, её удаление из модели приводит к её ухудшению.

Анализ остатков:

Проверка остатков на независимость

Провели анализ остатков (на вкладке Residuals/assumptions/prediction использовали кнопку Perform residuals analysis):

Проанализировали остатки на независимость (тест Дарбина-Уотсона, вкладка Advanced / Durbin-Watson statistic);

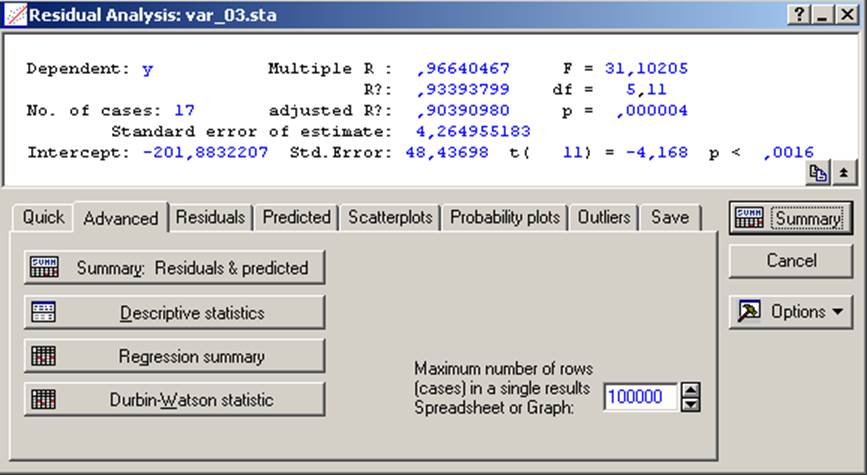
Рисунок 9

Тест Дурбина-Уотсона представлен в таблице 11

Таблица 11 - Тест Дурбина-Уотсона

Тест Дарбина-Уотсона: значение ~2, что говорит о независимости остатков в рассматриваемом примере.

Проверка остатков на соответствие нормальному распределению

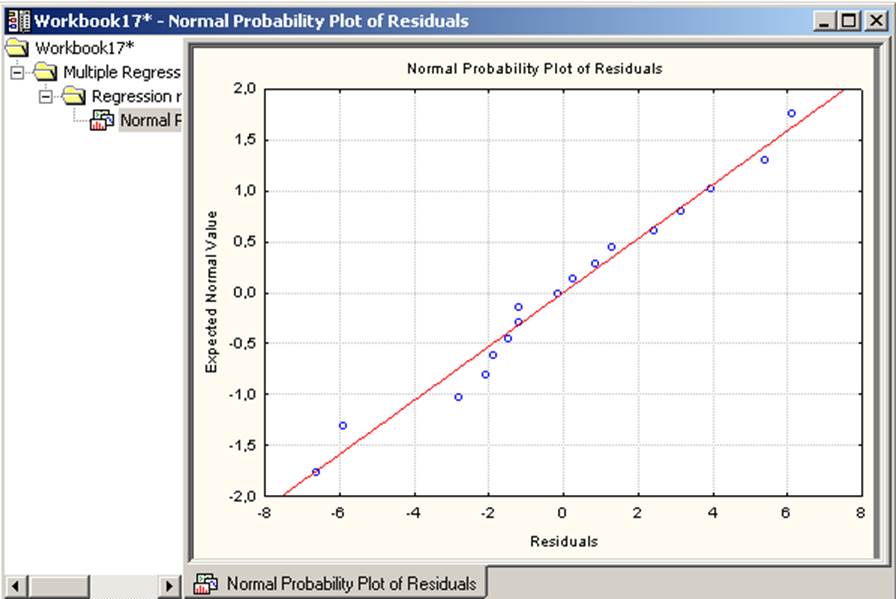
Рисунок 10.Проверка соответствия остатков нормальному распределению

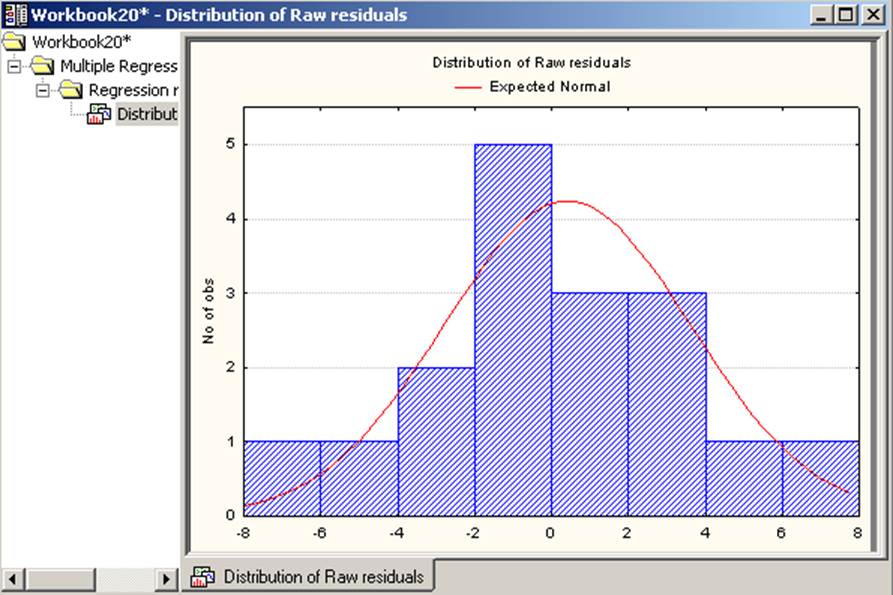
Рисунок 11. Гистограмма остатков

Из полученных графиков можно предположить, что условие нормальности соблюдается. Однако, для более точной проверки соблюдения условия нормальности остатков следует использовать модуль Подгонка распределения (Distribution fitting, см. лаб. раб. 1). Значения остатков можно посмотреть в таблице Summary: Residuals & Predicted, столбец Residual.

Таблица 12 - Значения остатков

	Observed	Predicted	Residual	Standard	Standard	Std.Err.	Mahalanobis
1	71,05000	69,75252	1,29749	0,46489	0,30422	1,873870	2,14748
2	62,68000	63,89634	-1,21633	0,02445	-0,28519	3,234047	8,25873
3	61,51000	61,68058	-0,17058	-0,14219	-0,04000	2,259198	3,54834
4	52,75000	54,85867	-2,10867	-0,65525	-0,49442	2,218363	3,38751
5	54,96000	54,71095	0,24905	-0,66636	0,05839	2,122706	3,02225
6	50,22000	56,85099	-6,63098	-0,50541	-1,55476	2,395529	4,10653
7	61,49000	60,64296	0,84704	-0,22023	0,19861	2,914447	6,53025
8	84,74000	81,62391	3,11609	1,35772	0,73063	1,939156	2,36645
9	78,23000	81,02554	-2,79554	1,31271	-0,65547	1,966961	2,46199
10	67,92000	62,52842	5,39158	-0,07842	1,26416	2,597746	4,99470
11	89,67000	83,54796	6,12204	1,50242	1,43543	2,227626	3,42374
12	54,69000	55,90221	-1,21221	-0,57677	-0,28423	3,040026	7,18798
13	63,27000	65,15660	-1,88660	0,11924	-0,44235	2,678556	5,36974
14	82,05000	87,95350	-5,90350	1,83375	-1,38419	2,616852	5,08233
15	55,30000	51,34227	3,95773	-0,91972	0,92797	2,538846	4,72857
16	39,66000	41,14252	-1,48253	-1,68682	-0,34761	3,597014	10,43969
17	50,52000	48,09407	2,42593	-1,16401	0,56880	2,101575	2,94373
Minimum	39,66000	41,14252	-6,63098	-1,68682	-1,55476	1,873870	2,14748
Maximum	89,67000	87,95350	6,12204	1,83375	1,43543	3,597014	10,43969
Mean	63,57118	63,57118	-0,00000	0,00000	-0,00000	2,489560	4,70588
Median	61,51000	61,68058	-0,17058	-0,14219	-0,04000	2,395529	4,10653

Рисунок 12. Проверка соответствия остатков нормальному распределению

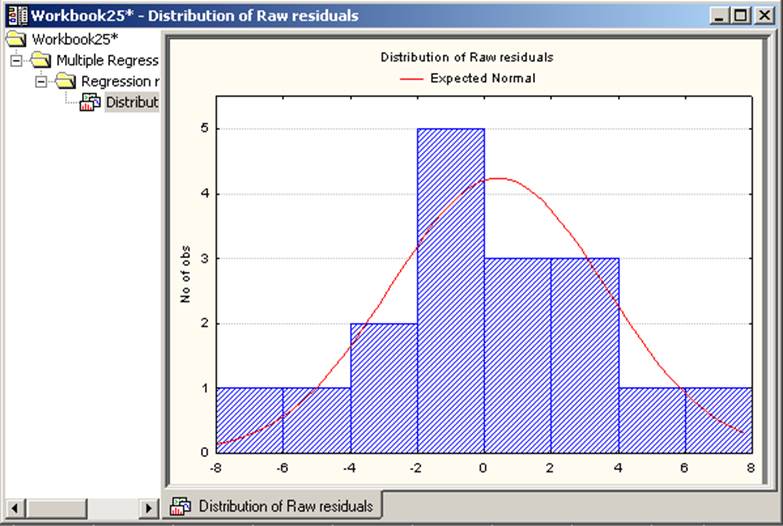
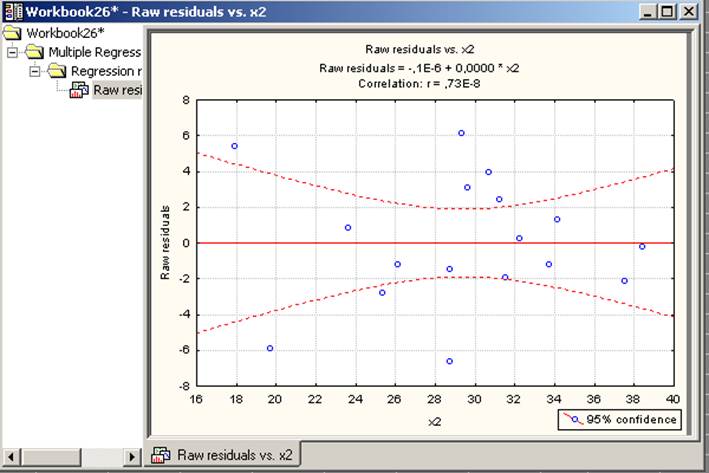
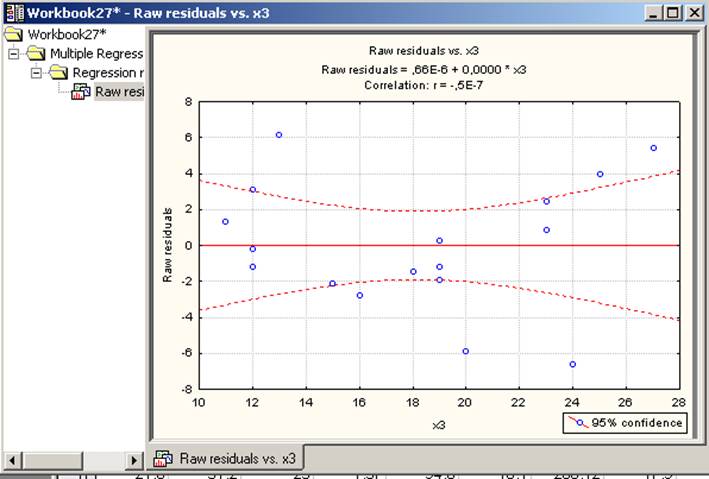
На основе анализа графиков остатков от всех независимых переменных, можно сделать вывод, что в рассматриваемом примере остатки отвечают предположению линейной зависимости эндогенной переменной от экзогенных.

7.3.  Определили зависимости эндогенной переменной от экзогенных переменных с помощью модуля «Множественная регрессия» и методом автоматической регрессии определили переменные, оказывающие решающее влияние на эндогенную переменную. Результат представлен на рисунке

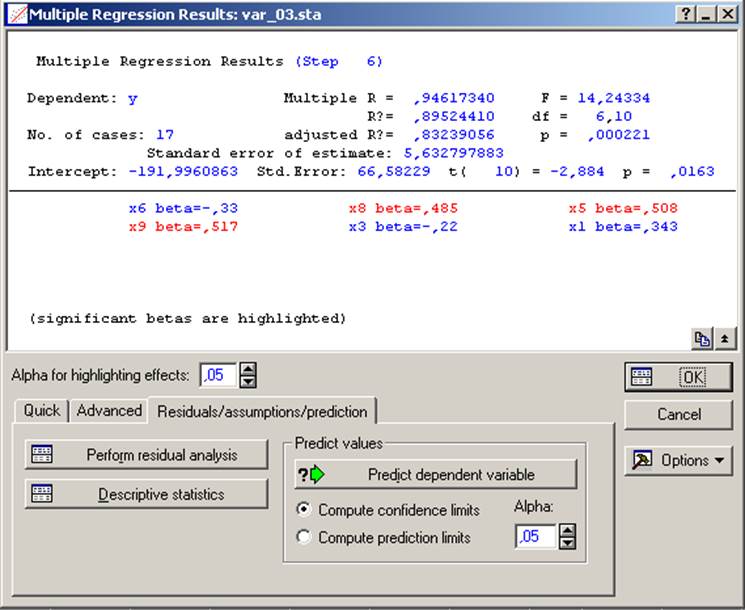
Рисунок 13. Результат автоматической пошаговой регрессии

Вывод: в результате автоматической пошаговой регрессии выявили значимые переменные х5, х8 и х9. Первые из них соответствуют результату пошаговой неавтоматической регрессии.