Разведывательный анализ данных и регрессионный анализ средствами пакета STATISTICA, страница 2

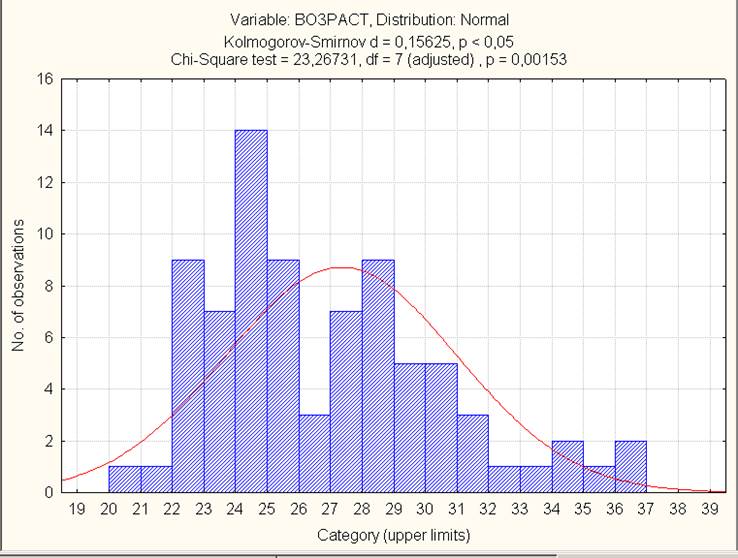
Рисунок 6. Проверка гипотезы о нормальном  распределении

Гипотеза  не подтвердилась.

Проверяем другие распределения и приходим к выводу, что переменная возраст имеет распределение Log-normal.

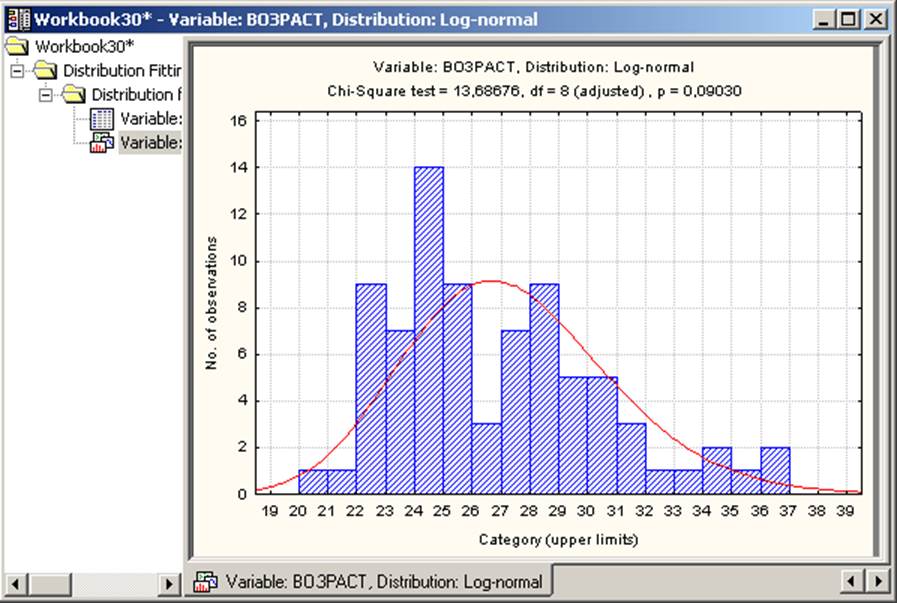
5. Проверили гипотезы о равенстве математических ожиданий для переменных «Возраст» и «Естест-науч лит-ра» заданным значениям с помощью одновыборочного t-теста.  Результат представлен в таблице 3.

Таблица 3 – Проверка гипотез

T-test for Dependent Samples (new1.sta)
Marked differences are significant at p < ,05000
					Std.Dv.
	Mean	Std.Dv.	N	Diff.	Diff.	t	df	p
ВОЗРАСТ	27,35	3,663366
ЕСТ_НАУЧ	0,4025	0,270786	80	26,9475	3,843411	62,71143	79	0

Используя двухвыборочный t-критерий проверили гипотезу о равенстве мат. ожиданий двух выборок. В качестве группирующей переменной взяли «Возраст», в качестве второй переменной взяли «Активность». Результат представлен в таблице 4.

Таблица 4 – Проверка гипотез

Grouping: ВОЗРАСТ (new1.sta)
Group 1: G_1:1
Group 2: G_2:2
	Mean	Mean				Valid N	Valid N	Std.Dev.	Std.Dev.	F-ratio	p
	G_1:1	G_2:2	t-value	df	p	G_1:1	G_2:2	G_1:1	G_2:2	variancs	variancs
АКТИВН				0		0	0

6. Вычислили корреляционную матрицу для исследуемых выборок, сделали вывод о наличии (или отсутствии) линейной зависимости между случайными величинами, соответствующих данным выборкам.

Результат представлен в таблице 5 и на рисунке 6.

Таблица 5 – Корреляция

Correlations (new1.sta)
Marked correlations are significant at p < ,05000
N=80 (Casewise deletion of missing data)
	ЕСТ_НАУЧ
ВОЗРАСТ	-0,64427

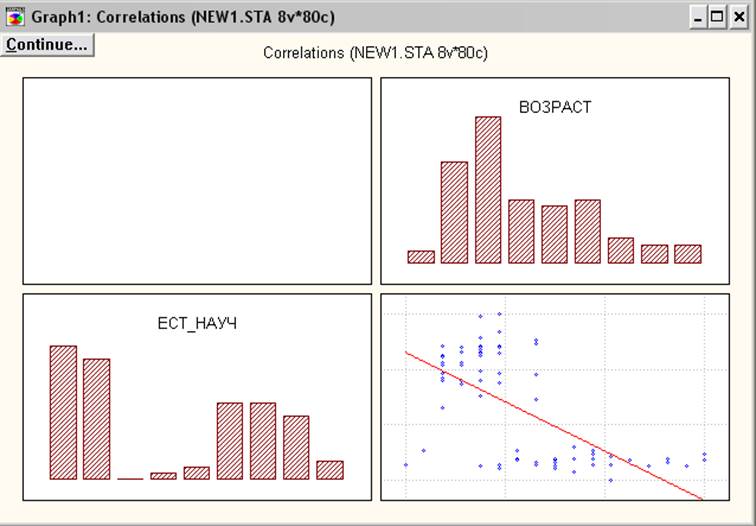
                                                    Рисунок 7. Корреляционная матрица

Можно сделать вывод, что между двумя переменными существует сильная отрицательная  связь.

7. Провели регрессионный анализ данных.

7.1. Исследовали зависимость эндогенной/зависимой переменной от экзогенных/независимых переменных с помощью модуля Correlation matrices (пункт меню Основные статистики/Таблицы (Basic Statistics/Tables)).

 7.1.1. Построили корреляционную матрицу. Исходя из полученных результатов, сделали предположение о том, что параметр Х6 оказывают наибольшее влияние на эндогенную переменную. Результат представлен в таблице 6.

Таблица 6 – Зависимости переменных

	x1	x2	x3	x4	x5	x6	x7	x8	x9
y	0,47	-0,29	-0,40	0,22	0,52	-0,62	-0,02	0,27	0,09

7.1.2. Проанализировали матрицы парных коэффициентов корреляции экзогенных переменных, и сделали предварительные предположения о наличии мультиколлинеарности объясняющих переменных.

Параметр X7 оказывает наименьшее влияние. Связь между У и X2, X3, Х6, Х7 носит отрицательный характер.

7.2. Исследовали зависимости эндогенной переменной от экзогенных переменных с помощью модуля Multiple Regression (Множественная регрессия) и методом пошаговой регрессии определили переменные, оказывающие решающее влияние на эндогенную переменную.

7.2.1.  Выполнили первую итерацию метода пошаговой регрессии.

-  Задали  зависимую и независимые переменные

-  Рассмотрели все объясняющие переменные (Multiple R, R?, adjusted R?, Standard error of estimate, Intercept, F, df), Результат представлен на рисунке 8.

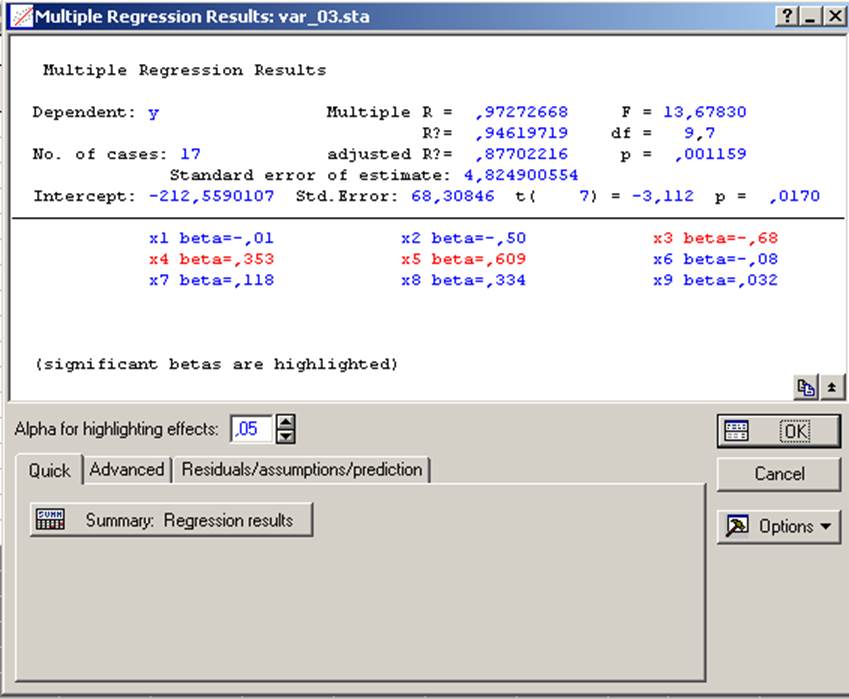
Рисунок 8. Результат первого шага пошаговой регрессии

Анализ полученных результатов:

-  Коэффициент детерминации R? = 0,946, т.е. в рассматриваемом примере около 95%  разброса объясняется регрессией, а 5% объясняется ошибками регрессии.

-  Коэффициент множественной корреляции Multiple R = 0,973 (корень квадратный из R?)описывает связь между предсказываемой переменной  и линейной комбинацией предикторов (для парной регрессии он совпадает с абсолютным значением коэффициента корреляции).