Правильность организации измерений, обеспечивающих достижение требуемой точности и достоверность результатов оценки свойств объектов, страница 26

Δφ_s  = ( l – l³ /6) l1 - l1α

Синусный рычаг совершает симметричные отклонения от среднего положения в пределах α = ± π / 24.

При этом величина систематической погрешности

Δφ_s = 0,003 l1

Приведем график систематической погрешности синусного механизма при фиксированном перемещении α.

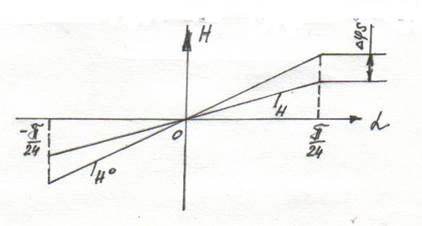
Рис.  график схемной погрешности

Систематическая погрешность в середине шкалы равна нулю (т.к. sinα_о = 0),а на краях шкалы она имеет максимальное значение.

Заданный закон связи параметров синусного механизма  

Н^о = lо α

выражается через постоянный размер lо  синусного рычага. Анализ выражения систематической погрешности Δφ_s показывает, что снижение  Δφ_s  для фиксированных значений α может быть достигнуто по переменной l1.

Значение l1 обеспечивающее минимум систематической погрешности на начальной и конечной отметках шкалы, определяется из уравнения  Δφ_s = 0.

Используемые функции синусного механизма отвечают условию симметричности. Функция положения φ и заданная функция  φ° симметричны относительно нулевого значения шкалы.

Рассматриваемый измерительный механизм образован с помощью синусного и тангенсного элементарных механизмов, последовательно соединенных между собой.

Требование симметричности должно соблюдаться для всех механизмов, образующих измерительную цепь.

Тангенсный механизм подобран с таким расчетом, чтобы его функция положения в определенной мере компенсировала систематическую погрешность синусного механизма. В двухрычажном механизме происходит внутренняя компенсация систематической погрешности синусного механизма за счёт тангенсного. Ускоренное движение рычага  синусного механизма компенсируется замедленным перемещением ведомого рычага тангенсного механизма.

После установления элементарной структуры общего измерительного механизма решается задача определения его общей систематической погрешности.

С этой целью рассмотрим частную функцию положения двухрычажного механизма φ данной кинематической схемы до её зубчатой части.

φ=	arcsin	H L	-	arcsin	H
		l1 l2			l1

где φ – угловое перемещение тангенсного рычага ( l2) в радианах, выраженное через перемещение синусного рычага (l1) .

Функцию положения двухрычажного механизма представим в виде отрезка степенного ряда, ограничив разложение тремя членами. (n =3)

φ=	(	L	-	1	)	H	+	1	[	(	L	)³	-	1	]	H³
		l2				l1		6			l2					l1 ³

При этом передаточное отношение i₁  двухрычажного механизма:

i1=	L - l2
	l1 l2

Определим передаточное отношение i₂ , связывающее перемещение стрелки относительно штрихов шкалы с угловым перемещением тенгенсного рычага ( l₂ );                           

i2=	z1	Rстр
	z2

где z₁ – число зубьев зубчатого сектора (ведущее звено);

z₂  - число зубьев триба (ведомое звено);

R стр – длина указателя (стрелки), мм;

Передаточное отношение i₂ имеет размерность мм/рад. Для проектируемой рычажно-зубчатой головки принято:

   z₁= 228;  z₂  = 16;  R стр = 22 мм.

С учётом этого

i₂= 313,5 [мм/рад].

Таким образом, выражение общей функции положения рычажно-зубчатого механизма примет вид:         

φ(о)=	313,5	{	(	L	-	1	)	H	+	1	[	(	L	)³	-	1	]	H³	}мм
				l2				l1		6			l2					l31