Уравнения Беллмана позволяют рассчитать всю последовательность значений ωk(Х), начиная с Xm, Um вплоть до Х0 — произвольного начального состояния. При этом расчете U(X, t) может интерпретироваться как оптимальный закон управления с обратной связью по измерениям текущего (шаг k) состояния объекта.
Из сказанного очевидна следующая особенность метода динамического программирования — с его помощью решается не одна конкретная задача при определенном Х0, а сразу все подобные однотипные задачи при любом начальном состоянии.
Численная реализация метода динамического программирования весьма сложна и применяют его обычно в тех случаях, когда необходимо многократно решать типовые задачи, например такие, как определение оптимального режима полета самолета при меняющихся погодных условиях. Основная идея метода динамического программирования переносится и на непрерывные во времени системы автоматического управления.
Рассмотрим вновь оптимальную задачу
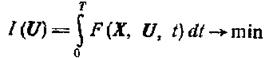(1.13-14.67)
на траекториях системы
(1.13-14.68)
Введем функцию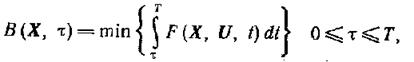 
(1.13-14.69)
где минимизация производится при условиях
(1.13-14.70)
Выведем уравнение Беллмана (иногда это уравнение называют уравнением Беллмана - Гамильтона - Якоби в силу аналогии со сходным уравнением Гамильтона - Якоби в аналитической механике) в этом случае, имея в виду, что оптимальное значение критерия
(1.13-14.71)
Рассмотрим два момента времени τ и τ+Δ, Δ > 0. Согласно определению В(Х, τ) имеем
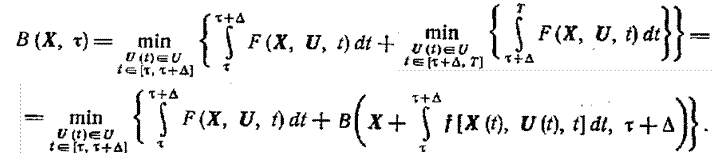(1.13-14.72)
Здесь вновь используется основная идея метода динамического программирования, дающая возможность провести сначала выбор управления, начиная с момента τ+Δ до Т, а затем осуществить минимизацию по значениям управления в пределах отрезка [τ, τ+Δ].
Считая, что функции F(X, U, t) и f(X, U, t) непрерывны по всем аргументам, допустимые траектории X(t) непрерывны по t и U(t) принадлежат к классу кусочно-непрерывных функций, причем отрезок [τ, τ+Δ] не включает точек разрыва, имеем с точностью до членов более высокого порядка малости по Δ:
(1.13-14.73)
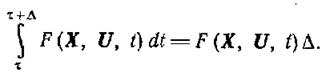(1.13-14.74)
Считая, что функция В(Х, τ) дифференцируема, разложим ее в ряд Тейлора, пренебрегая более высокими членами малости, чем Δ:
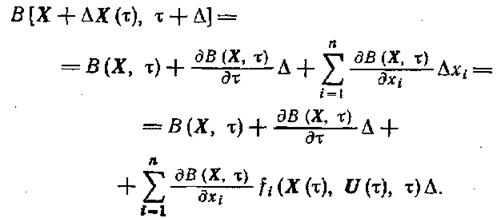(1.13-14.75)
Подставив (1.13-14.57), (1.13-14.58), (1.13-14.59) в (1.13-14.56) и заменяя τ на t, получаем искомое уравнение Беллмана в непрерывном случае:
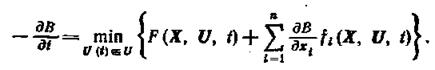(1.13-14.76)
Так же как и в дискретном случае, важно понимать, что функция U(X, t), минимизирующая выражение
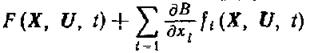(1.13-14.77)
по явно входящему U в пределах допустимой области U при фиксированных X и t, определяет оптимальный закон управления с обратной связью по измерениям текущего состояния системы X=X(t).
Сравнивая
выражения (1.13-14.77.) с основным условием принципа максимума Понтрягина (1.13-14.52),
нетрудно усмотреть, что, обозначив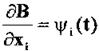 
и определив функцию Гамильтона, как и ранее,
приходим к требованию ее максимизации при U(t) c U.
В заключение необходимо отметить, что рассмотренный нами материал сложен, и это надо ясно себе представлять. Строгое его изложение потребовало бы знаний функционального анализа и топологии, а, кроме того, значительного объема работы. Хотя название курса вроде бы неявно подразумевает обучение некоей вычислительной технике решения задач автоматического управления, следует все же различать основополагающие идеи, заложенные в тот или иной метод и технику его численной реализации. Нами основной акцент сделан именно на идеях, в них заложенных, вернее, на развитии идеи Лагранжа, цитируемой выше. Вычислительная же техника этих методов — это умение составления корректных алгоритмов, реализация которых возможна, как правило, только на самых современных и мощных ЭВМ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.