(1.13-14.17)
которые необходимо решить относительно (x1, х2, ..., хn), (λ0, λ 1, λ 2, ..., λ m) и среди этих решений выбрать нужное.
Из сформулированных ранее теорем следует, что если совокупность (множество) допустимых точек ограничена и все функции f0, f1, ..., fm непрерывны вместе со всеми частными производными, то описанное правило приведет к решению задачи.
Сделаем несколько замечаний. Во-первых, условия (1.13-14.16.) и (1.13-14.17.) дают n+m уравнений c n+m+1 неизвестными. Однако надо иметь в виду, что множители Лагранжа можно умножить на любую константу, отличную от нуля, т. е. всегда считать один из множителей Лагранжа равным единице. Тогда число уравнений в (1.13-14.16.) и (1.13-14.17.) фактически равно числу неизвестных. Во-вторых, уравнения (1.13-14.16.) содержательны с точки зрения нахождения экстремума, только если λ0≠0. Ведь если λ0=0, то уравнения (1.13-14.16.) отражают лишь вырожденность ограничений и не связаны с функцией, экстремум которой ищется.
Выше была рассмотрена задача нахождения экстремума при ограничениях типа равенств. Естественно, было бы следующим шагом рассмотреть более общий случай, когда ограничения могут иметь вид равенств и неравенств. Однако эта задача в общем случае столь сложна, что ей посвящены исследования целого раздела современной математики, называемого математическим программированием. Для более подробного изучения математического программирования отсылаем интересующихся к литературе: Зуховицкий СИ., Авдеев Л, И. Линейное и выпуклое программирование. М.: Наука, 1986; Карманов В.Г. Математическое программирование.- М.: Наука, 1986.
1.13-14.2. Начала
вариационного исчисления.
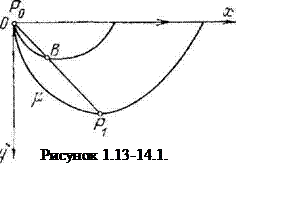
В июньском номере первого научного журнала «Акта Эрудиториум» за 1696 год была помещена заметка знаменитого Иоганна Бернулли — «Новая задача, к решению которой приглашаются математики», ставшая отправной вехой развития вариационного исчисления. Эта задача, которую обычно называют задачей о брахистохроне (по-гречески — наибыстрейшей), заключается в следующем: между точками Р0 и P1 (рисунок 1.13-14.1.) провести кривую таким образом, чтобы время падения тела, движущегося без трения по кривой Р0 и P1 под действием силы тяжести, было минимальным. Формализация этой задачи следующая:
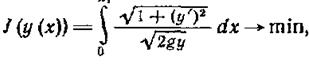(1.13-14.18.)
(1.13-14.19)
Формула 1.13-14.18 легко получается из закона сохранения энергии mgy = V2/2 и соотношения dS = (1+(у´)2)1/2, где dS - длина малого участка кривой у(х)
Следует обратить внимание, что в этой задаче отыскивается, в отличие от вышеизложенного, не точка или множество точек, в которых функция достигает экстремума, а некая функция (в данном случае некая кривая), на которой J(y(x)) достигает экстремума.
Выражение J(y(x)), задаваемое формулой (1.13-14.18), является типичным примером, иллюстрирующим понятие функционала. Функционалом называется функция, определенная на некотором множестве функций.
Например, интеграл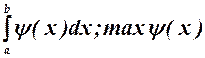 
при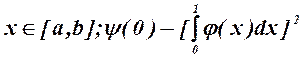 
и т. д.
Иногда говорят, что функционал есть функция бесконечного числа переменных. Так же, как и обычная функция, функционал имеет область определения. Такой областью, например, может быть совокупность (в математике чаще говорят - пространство или класс) всех непрерывных функций на отрезке [а, b]. Это пространство обозначают С0([а, b]). Другая область - пространство С1([0, b]), с которым на протяжении двух веков имеет дело вариационное исчисление: С0([а, 0]) - это пространство непрерывно дифференцируемых на отрезке [а, b] функций.
Заметим, что весьма существенно, в каком классе (пространстве) ищется экстремум. Так, он может существовать в одном классе и не существовать в другом. Очевидно, что для определения понятия локального экстремума функционала необходимо ввести «меру близости» функций в рассматриваемых нами пространствах С0([0, b]) и С1([а, b]). Аналогом расстояния между двумя функциями в каждом из рассматриваемых классов является норма разности этих функций. Понятие нормы в этих пространствах определяется следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.