Задачи оптимального управления. Экстремумы функций. Принцип Лагранжа, страница 7

(1.13-14.50)

Обычно принцип максимума Понтрягина формулируют, используя функцию Гамильтона (см. (1.13-14.28.)). При этом наряду с системой (1.13-14.47) рассматривают сопряженную систему

                                      (1.13-14.51)

ψ_i(t) - точно такие же множители Лагранжа, как и λ(t). Справедлива следующая теорема.

Принцип максимума Понтрягина. Для того чтобы вектор-функция U(t) доставляла минимум функционалу

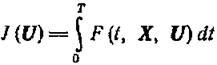
при условиях

необходимо, чтобы она доставляла максимум функции Гамильтона, т. е. чтобы она была решением задачи

               (1.13-14.52)

К условию (1.13-14.52) должны быть добавлены еще граничные условия

                                        (1.13-14.53)

В сделанных предположениях данная теорема позволяет свести задачу отыскания оптимальной программы к краевой задаче для системы обыкновенных дифференциальных уравнений. Действительно, из условия (1.13-14.52) можно определить управление U как функцию ψ, X, t, т.е.

                                            (1.13-14.54)

Подставив эту функцию в (1.13-14.35) и (1.13-14.51) получим систему уравнений

    (1.13-14.55)

где компоненты вектор-функции φ* определяются из (1.13-14.51). Учитывая граничные условия (1.13-14.53), имеем систему из 2n уравнений с 2n граничными условиями. Напомним, что n - размерность фазового вектора.

Сформулированная теорема — принцип максимума Понтрягина — говорит о том, что оптимальная программа может содержаться только среди решений краевой задачи (1.13-14.53), (1.13-14.55).

Процедура решений этой задачи заключается в решении экстремальной задачи (1.13-14.52), где вектор управления имеет размерность m. Эта задача должна решаться на каждом шаге численного интегрирования системы (1.13-14.55), т.е. в данном случае принцип максимума Понтрягина позволяет свести решение задачи размерности mxN (N -число интервалов интегрирования) к решению N задач размерности m, связанных процедурой численного интегрирования.

Проиллюстрируем вышесказанное на одном и наиболее популярных методов решения задач оптимального управления, носящем название метод пристрелки. Суть его заключается в процедуре подбора ψ(0) таким образом, чтобы достигнуть цели управления Х(Т)=Х_Т, исходя из начального состояния системы Х(0)=Х₀. Предположим, что ψ(0)=ψ₀, и применим схему Эйлера, описанную в предыдущем разделе, т.е. зададим шаг интегрирования m и положим

          (1.13-14.56)

В частности,

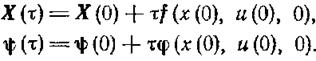                           (1.13-14.57)

Согласно принципу максимума для определения Х(Т) и ψ(Т) нужно найти управление u(0) такое, что достигается

                          (1.13-14.58)

Заметим, что если u - открытое множество, то, как и ранее, для решения задачи (1.13-14.58) можно использовать необходимые условия максимума функции, которые приводят к решению, как правило, системы трансцендентных урaвнeний

                               (1.13-14.59)

(см. также (1.13-14.30.)).

Определив u(0) из условия (1.13-14.58), находим из (1.13-14.57) величины Х(Т) и ψ(Т). Повторяя эту процедуру, можно найти последовательно значения Х(2Т) и ψ(2Т), Х(3Т) и ψ(3Т) и т. д. Окончанием этой процедуры является нахождение вектора Х(Т). Поскольку величина ψ(Т) выбиралась произвольным образом, то при t=Т в общем случае

                                       (1.13-14.60)

ясно, что Ф будет функцией от ψ(0), т.е. Ф=Ф(ψ(0)) и, следовательно, задача будет решена, если удастся подобрать ψ(0) для которого

                                                 (1.13-14.61)

Таким образом, в итоге метод пристрелки приводит к решению хорошо разработанной задачи отыскания нулей некоторой вектор-функции. Несмотря на кажущуюся простоту метода пристрелки, в нем содержится много подводных камней, связанных с его численной реализацией.