Задачи оптимального управления. Экстремумы функций. Принцип Лагранжа, страница 5

          (1.13-14.27.а)

и минимизирующую функционал

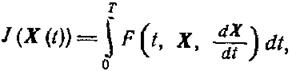                               (1.13-14.28.а)

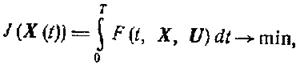                                       (1.13-14.28.b)

где

Функция               

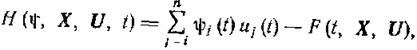
где Ψ(t) = {ψ₁(t), ψ₂(t),..., ψ_n(t)} - некоторая вектор-функция, заданная на отрезке [0, Т], называется функцией Гамильтона для задачи (1.13-14.27.), (1.13-14.28.).

Как вытекает из вышеизложенного, необходимое условие достижения минимума функционала J(X(t)) может быть сформулировано следующим образом. Пусть функция F(t,X,U) непрерывно дифференцируема, как функция своих аргументов. Если непрерывно дифференцируемая вектор-функция х°(t) является решением задачи, то существуете непрерывная вектор-функция Ψ°(t) = {ψ°₁(t), ψ°₂(t),..., ψ°_n(t)} такая, что пара Х°(t), Ψ°(t) удовлетворяет следующим условиям:

1.13-14.3. Прямые методы решения задач оптимального управления.

При знакомстве с основными понятиями теории автоматического управления упоминалось в общих чертах о задачах оптимального управления. Кратко вспомним.

Оптимальная программа Х°, U° определяется как решение вариационной задачи

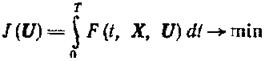                         (1.13-14.34)

при условиях

                                        (1.13-14.35)

                                            (1.13-14.36)

где U — фиксированное множество векторов управления, U(t) принадлежит к не которому классу функций

                               (1.13-14.37)

Напомним, что вектор-функция U — находящееся в нашем распоряжении управление.

Методы расчета оптимальных программ принято разделять на два класса. К первому относятся прямые методы, которые используют тот или иной способ редукции (сведения сложного к более простому) вариационной задачи (1.13-14.34.)-(1.13-14.37.) к конечномерной задаче математического программирования. Ко второму классу относятся методы, использующие необходимые условия. Эта классификация достаточно условна, так как при решении конкретных задач оба класса методов часто дополняют друг друга, тем не менее, она удобна, поскольку показывает существенное различие в подходах к решению рассматриваемых задач.

Проиллюстрируем это на простейшем примере отыскания минимума функции f(X). Прямые методы (в научной литературе эти методы носят названия методов спуска. Среди них выделяют метод градиентного спуска, метод оврагов и др.) основываются на идее построения некой итерационной последовательности

                                       (1.13-14.38)

где g^k - вектор, указывающий некоторое направление убывания функции f в точке X_k, a α_k - итерационный параметр, величина которого указывает длину шага в направлении g^k. Обычно в качестве вектора g^k выбирают вектор 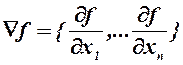противоположный градиенту f(X), который, как известно, является нормалью к поверхности уровня f(X)=с (с - некая константа) в сторону наибольшего уменьшения функции.

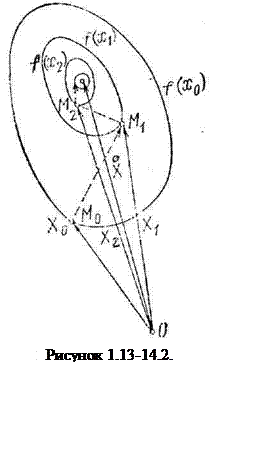
Схематически вычислительная процедура строится следующим образом. Пусть Х° - вектор (точка в n-мерном пространстве), задающий минимум f(X), а Х₀ - его нулевое приближение. Через точку Х₀ (точка М₀) проведем поверхность уровня функции f(X)=f(X₀). Если точка Х₀ достаточно близка к искомой точке X, то поверхность уровня f(X)=f(X₀) будет похожа на эллипсоид.

Из точки Х₀ двигаемся по нормали к этой поверхности в сторону убывания до тех пор, пока эта нормаль не коснется в некоторой точке X₁ какой-либо другой поверхности уровня (рисунок 1.13-14.2.): f(X)=f(X₁). Затем, отправляясь от точки X₁, вновь повторяем эту процедуру и т. д. Так как f(X₀) > f(X₁) > f(X₂), ..., то, двигаясь по такому пути, мы быстро приближаемся к наименьшим значениям f(X°) (дно «ямы»). Величину шага α_k на каждой итерации обычно выбирают из условия

                  (1.13-14.39)

находя наименьшее положительное α.