Задачи оптимального управления. Экстремумы функций. Принцип Лагранжа, страница 4

                       (1.13-14.20)

                           (1.13-14.21)

Используя понятие нормы, определим локальный экстремум по аналогии с определением 1.13-14.1.2.

Определение 1.13-14.2.1. Функция у°(х) доставляет локальный максимум (минимум) функционалу J(y), если можно указать такое ε>0, что для всех функций, принадлежащих классу С¹{[а, b]}, при выполнении неравенства

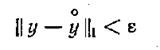                                           (1.13-14.22)

выполняется неравенство

                                 (1.13-14.23)

Аналогично тому, как это делают в случае функций, число J(y) называют наибольшим (абсолютный максимум) или наименьшим (абсолютный минимум) значением функционала, если

                          (1.13-14.24)

для любых у(х)Î С¹{[а, b]}.

1.13-14.2.1. Простейшая задача вариационного исчисления (задача Лагранжа).

Обобщением задачи о брахистохроне является - задача Лагранжа: найти функцию x(t)ÎС¹{[0, Т]}.удовлетворяющую граничным условиям

                           (1.13-14.25)

которая минимизирует функционал вида

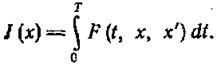                                 (1.13-14.26)

Прежде чем перейти к решению этой задачи, сделаем два замечания. Во-первых, все приводимые ниже выкладки легко обобщаются на случай, когда x(t) — не скалярная, а векторная функция. Во-вторых, эту задачу можно интерпретировать с точки зрения автоматического управления, как выбор некой программной траектории, минимизирующей затраты (например, топлива) при переводе объекта управления из начального состояния в фазовом пространстве Х(0) = Х₀ в заданное конечное состояние Х(Т) = Х₁ (например, вывод спутника на заданную траекторию).

Повторим путь, проторенный Лагранжем. Допустим, что функция F(t,x,y) в (1.13-14.26) (положим, x^о(t)=у) непрерывно дифференцируема, а функционал J(x) достигает локального минимума на непрерывно дифференцируемой кривой x(t). Возьмем теперь вариацию x^о(t), т.е. возьмем любую непрерывно дифференцируемую кривую x(t), которая обращается в нуль на концах:

                                        (1.13-14.27)

Тогда вариация x°(t), т. е. добавка к х^о(t) функции x(t), умноженной на любое число λ, не выводит нас из граничных условий (1.13-14.25.).

Исходя из сделанных выше предположений, функция одного переменного

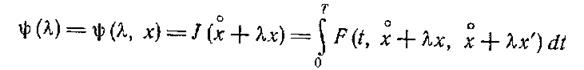  (1.13-14.28)

имеет локальный минимум в нуле, и, следовательно, для нее должна выполняться теорема Ферма, т. е.

                                                   (1.13-14.29)

В курсах математического анализа доказывается, что в сделанных выше предположениях при нахождении Ψ'(λ) возможно дифференцирование по λ под знаком интеграла. Таким образом, имеем

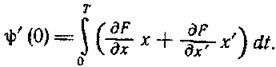                                 (1.13-14.30)

Проинтегрировав второй член в (1.13-14.30.) по частям с учетом (1.13-14.27.), получим

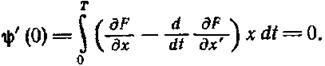.                        (1.13-14.31)

Уравнение (1.13-14.31.) должно выполняться при любой вариации x(t), что возможно лишь при выполнении условия

                            (1.13-14.32)

Это необходимое условие локального экстремума функционала J(x) называется уравнением Эйлера— Лагранжа. Его допустимые решения называются экстремалями. Экстремали в некотором смысле аналогичны стационарным точкам при нахождении экстремума функции.

Обобщением уравнения (1.13-14.32.), в случае если F = F(t, X, X'), где X = {x₁(t), ...., x_n(t)}, будет система из n уравнений вида

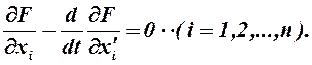                           (1.13-14.32.а)

Если в уравнении (1.13-14.32.) сделать замены

и ввести функцию Н=Ψ·U-F(t,X,U), то из уравнения (1.13-14.32.) и сделанных замен имеем

                                 (1.13-14.33)

Такое преобразование можем проделать и в случае, когда рассматривается задача Лагранжа от вектор-функции X(t) = {x₁(t), x₂(t), ..., x_n(t)},. Формализация этой задачи по аналогии с (1.13-14.27.)и (1.13-14.28.) следующая. Найти вектор-функцию X(t){x_i(t)}ÎС¹([0,T] (i=1, 2, n) удовлетворяющую граничным условиям