Задачи оптимального управления. Экстремумы функций. Принцип Лагранжа, страница 8

1.13-14.5. Оптимальное позиционное управление (динамическое программирование).

Среди задач оптимального управления различают задачи программного оптимального управления и позиционного оптимального управления. В первом случае управляющее воздействие U формируется в виде функции времени. Во втором случае управляющее воздействие U формируется в виде стратегии управления по принципу обратной связи, как функция от доступных значений фазового вектора состояний объекта управления (задача синтеза, о которой говорилось раньше).

Нахождение оптимального управления U°(t, X) сразу в виде функции текущего состояния связано с использованием метода динамического программирования. Этот метод представляет собой обширный раздел математики, посвященный решению многошаговых задач оптимального управления. При этом выбор управления на каждом шаге осуществляется в соответствии с конечной целью управления и состоянием системы, полученным в результате управления, принятого на предыдущем шаге.

В ряде задач автоматического управления многошаговость проистекает из существа процесса. Например, определение оптимальных размеров ступеней в многоступенчатой ракете. Часто многошаговость вводится искусственно, чтобы обеспечить возможность применения данного метода. Термин «динамическое» указывает на существенную роль времени и порядка в выборе управления.

Основная идея метода. Пусть процесс управления некоторой системой X состоит из m шагов. На i-м шаге управление U_i, переводит систему из состояния Х_i-1, достигнутого в результате (i-1)-го шага, в новое состояние Х_i. Этот процесс перехода осуществляет заданная функция f_i(X, U), и новое состояние определяется значениями Х_i-1, U_i:

                                                  (1.13-14.62)

Таким образом, управления U₁, U₂, ..., U_m переводят систему из начального состояния Х₀ в конечное состояние Х_Т, причем требуется, чтобы заданный функционал F(X₀, Ф₁, Х₁, Ф₂, ..., U_m, X_m) достигал экстремального значения F*, т.е., например,

                   (1.13-14.63)

Важной особенностью метода динамического программирования является то, что он применим лишь для аддитивной целевой функции. Это означает в данном примере, что

                                     (1.13-14.64)

В основе этого метода лежит принцип оптимальности, сформулированный Р. Беллманом. Этот принцип утверждает, что отрезок оптимальной траектории также является оптимальной траекторией. В применении к рассматриваемому примеру этот принцип может быть переформулирован следующим образом: предположим, что, осуществляя управление системой X, мы уже выбрали некоторые управления U₁, U₂, ..., U_k и тем самым траекторию X₁, X₂, ..., X_k и хотим завершить процесс, т. е. выбрать U_k+1, U_k+2, ..., U_m (а значит, и X_k+1, X_k+2, ..., X_m). Тогда, если завершающая часть процесса не будет оптимальной в смысле достижения максимума

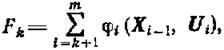                                (1.13-14.65)

то и весь процесс не будет оптимальным.

Используя этот принцип, получим основное функциональное соотношение метода динамического программирования, называемое уравнением Беллмана. Определим последовательность функций переменной Х:

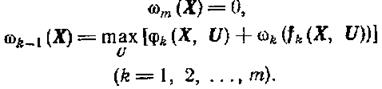                          (1.13-14.66)

Здесь максимум берется по всем управлениям, допустимым на шаге k. Смысл функций ω_k-1(Х) ясен: если система на шаге к-1 оказалась в состоянии X, то ω_k-1(Х) - максимально возможное значение функции F. Одновременно с построением функции    ω_k-1(Х) находятся условные оптимальные управления U_k(X) на каждом шаге, т. е. значения оптимального управления при всевозможных предположениях о состоянии Х системы на шаге k-1.