Задачи оптимального управления. Экстремумы функций. Принцип Лагранжа, страница 6

Второй класс методов, основанный на теореме Ферма, дающей необходимые условия экстремума, приводит в общем случае к решению трансцендентной системы уравнений

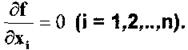
Каждый из этих методов имеет свои достоинства и недостатки, которые и определяют область их применения.

Рассмотрим один из возможных прямых методов расчета оптимальной программы для автономной, т. е. независящей явно от времени, системы автоматического управления. Будем изучать систему

                                                (1.13-14.40)

с функционалом

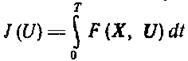                                                (1.13-14.41)

и граничными условиями

                              (1.13-14.42)

Ограничиваясь простейшей разностной схемой (схема Эйлера), заменим уравнение (1.13-14.40.) и функционал (1.13-14.41) следующими выражениями:

                                          (1.13-14.43)

                               (1.13-14.44)

где t_k = kτ, X(t_k) = Х_к, U(t_k) = U_k. К уравнению (1.13-14.43) должно быть добавлено начальное условие Х(0)=Х₀ и условие цели Х(Т)=Х_Т=X_N. Кроме того, на изменение управления и фазового вектора могут быть наложены и другие ограничения, типа U_kÎG_k, где G_k - некоторые множества.

Соотношения (1.13-14.43) позволяют произвести последовательное исключение фазовых векторов:

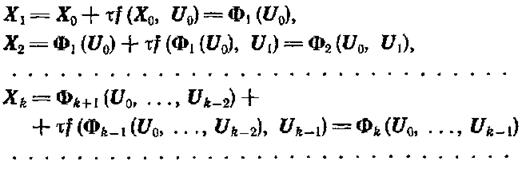
Таким образом, функционал (1.13-14.44) становится функцией только векторов U₀, ..., U_N-1:

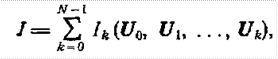                                 (1.13-14.45)

Где

Задача минимизации функционала (1.13-14.44) при ограничении U_kÎG_k, - стандартная задача математического программирования. Трудности решения этой задачи, как и многих других, однотипных с ней, в основном определяются ее размерностью, т.е. количеством переменных и количеством ограничений, на них налагаемых. В рассматриваемой выше схеме редукции число переменных определяется выбором количества интервалов N, что в свою очередь обусловливается требованиями точности. В технических задачах (динамика полета, запуск космических аппаратов и спутников, управление крупнотоннажными технологическими производствами и т. д.) число N достигает больших величин, и размерность задачи nxN (n - размерность фазового вектора) делает ее решение чрезвычайно трудоемкой. В подобных ситуациях на первый план выходят методы, которые используют необходимые условия, так как они мало чувствительны к увеличению числа интервалов разбиения.

1.13-14.4. Принцип максимума Понтрягина.

Начнем с самого простого примера задачи оптимального управления. Пусть F(t,X,U)=F_i(t)·u(t), где F_i(t) - непрерывная функция на отрезке [T,0]. Рассмотрим задачу

                          (1.13-14.46)

Совсем несложно понять, что изучаемый интеграл будет минимальным, если в случае F_i(t)·> 0 положить u(t)=1, т. е. u(t)= - signF₁(t).

По определению: sign t = 1 при t > 0:     =0 при t = 0:     = -1 при t < 0

И в более общей задаче

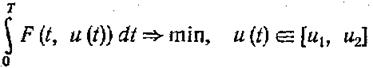                           (1.13-14.47)

следует поступать аналогично, а именно — надо для каждого tÎ [0, Т] найти и из отрезка [u₁, u₂] при котором функция F(t,u) имеет минимум по u. Это можно сформулировать в виде следующего утверждения: для того чтобы функция u(t) была решением задачи (1.13-14.47) необходимо, чтобы

                                 (1.13-14.47.а)

Теперь становится ясной идея, заложенная в принцип максимума Понтрягина. К задаче оптимального управления (1.13-14.34. и далее) применим общий замысел Лагранжа, только несколько модифицированный. Нужно, сняв ограничение в (1.13-14.36.), составить функцию Лагранжа, которая будет иметь вид

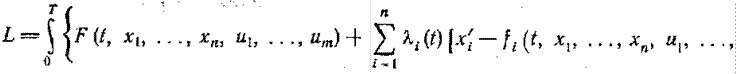
(1.13-14.48)

а затем рассмотреть задачу

              (1.13-14.49)

При этом необходимо по X, как и раньше, составить уравнение Эйлера, а по U применить утверждение типа (1.13-14.47). Но так как все члены с U в функции Лагранжа входят со знаком минус, то удобнее сформулировать это утверждение в виде принципа максимума. (Очевидно, что mах{- φ*}= - min{φ*}. Тогда решение задачи {x°₁(t), x°₂(t), ..., x°_n(t)},. {u°₁(t), u°₂(t), ..., u°_m(t)} будет удовлетворять условию