Вычислительная математика как часть математики

Введение

Вычислительная математика – это раздел математики, в котором разрабатываются методы доведения до числового результата решений основных задач математического анализа, алгебры и геометрии и пути использования для этой цели современных вычислительных средств.

Вычислительная математика как часть математики имеет древнюю и богатую историю, но в самостоятельную область вычислительная математика превратилась относительно недавно, в середине двадцатого века. Связано это как с необходимостью решения большого количества прикладных задач, так и с появлением вычислительной техники.

Так как вычислительная математика занимается доведением до числового результата решения задачи, то решение задачи должно существовать и быть единственным. Рассмотрим несколько простых примеров.

1) Рассмотрим систему линейных уравнений:

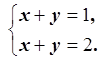
Эта система линейных уравнений не имеет решения. Любые  попытки решения этой системы методами вычислительной математики приведут к ситуации: «деление на ноль».

2) Система линейных уравнений:

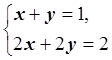
имеет бесконечное множество решений. Любые попытки решения этой системы методами вычислительной математики также приведут к ситуации «деление на ноль».

3) Система линейных уравнений

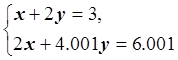
имеет единственное решение: x= 1, y= 1, которое легко может быть найдено различными методами вычислительной математики. Но что произойдет, если немного изменить правую часть последней системы линейных уравнений?

4) Рассмотрим систему линейных уравнений

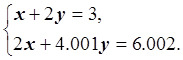
Эта система линейных уравнений имеет единственное решение: x= -1, y = 2. Сравним две последние системы линейных уравнений.

Их матрицы совпадают, правые части отличаются незначительно, но решения заметно отличаются друг от друга. Таким образом, незначительное изменение правой части привело к существенному изменению решения. Такие задачи называют неустойчивыми, и для их решения используют специальные методы вычислительной математики.

Как правило, мы будем рассматривать задачи, для которых одновременно выполняются следующие условия:

1)  решение задачи существует в некотором классе функций;

2)  решение задачи единственно в некотором классе функций;

3)  решение задачи непрерывно  зависит от входных данных, то есть малые изменения входных данных приводят к малым изменениям решения.

Такие задачи называются корректно поставленными. Если же хотя бы одно из этих условий не выполняется, то задача называется некорректно поставленной.

В вычислительной математике применяются различные методы, которые условно можно разбить на четыре группы: качественные, аналитические, методы возмущений и численные методы. В дальнейшем в основном мы будем рассматривать численные методы.

Численные методы – это такие методы решения задач вычислительной математики, которые сводятся или могут быть сведены к арифметическим действиям над числами.

Для решения задач мы будем строить вычислительные алгоритмы, которые в дальнейшем будут программироваться на ЭВМ.

Под вычислительным алгоритмом обычно понимается последовательность операций (логических и арифметических), при помощи которых находится решение задачи вычислительной математики.

Сложность вычислительного алгоритма – это ресурсы ЭВМ, необходимые для реализации алгоритма. Ресурсы – это время счета и используемая память ЭВМ.

Время работы программы пропорционально числу арифметических действий, поэтому сложность вычислительного алгоритма по времени оценивается числом арифметических действий, необходимых для реализации алгоритма.

Вычислительный алгоритм называется устойчивым, если ошибки округления на ЭВМ при реализации этого алгоритма будут сказываться незначительно. В противоположном случае (когда ошибки округления могут неограниченно возрастать) вычислительный алгоритм называется неустойчивым.

Основные требования к вычислительному алгоритму:

1)  вычислительный алгоритм должен давать единственное решение задачи с заданной точностью за конечное число шагов либо вывод о невозможности получения решения;

2)  вычислительный алгоритм должен быть устойчивым;

3)  сложность вычислительного алгоритма должна быть минимально возможной.

В рамках дисциплины студентами специальности 220400 “Программное обеспечение вычислительной техники и автоматизированных систем”, обучающимися в течение 5 лет, выполняются три расчетно-графических задания, но студентами этой специальности, обучающимися 3,5 года, выполняются два расчетно-графических задания, а именно: второе и третье РГЗ. Номер варианта определяется  по двум последним цифрам номера зачетной книжки. Две последние цифры в диапазоне от 00 до 29 соответствуют с 01 по 30 варианты. Для диапазона от 30 до 59 от номера зачетной книжки следует вычесть 30, от 60 до 89 – вычесть 60 и от 90 до 99 – вычесть 90.

Отчет по каждому расчетно-графическому заданию сдается в бумажном виде на листах формата А4. Отчет включает в себя титульный лист, задание, алгоритм, текст программы на языке программирования Си, результат работы программы и список литературы.

После изучения курса студенты сдают письменный экзамен. Экзаменационный билет составляется из задач, аналогичных рассмотренных в п.п. 1.7, 2.9, 3.12, 4.5, 5.8, 6.8 и 7.9 данного пособия.