Вычислительная математика как часть математики, страница 5

Отметим, что в дальнейшем мы будем для пространства n раз непрерывно дифференцируемых функций на отрезке [a, b] использовать обозначение: . Если функция f является непрерывной функцией на отрезке [a, b], то это можно записать так: . Если функция f является непрерывно дифференцируемой на отрезке [a, b], то это можно записать следующим образом: . Если f – дважды непрерывно дифференцируемая функция на отрезке [a, b], то будем использовать обозначение:  и т.д.

2.3. Уточнение корня

Постановка задачи уточнения корня

Пусть известен отрезок [a, b], который содержит один корень уравнения f(x) = 0. Пусть с – точное значение корня , c Î [a, b]. Требуется найти число , для которого выполняется следующее неравенство: , где e – заданная точность. Число  называется приближенным значением корня с точностью e.

В дальнейшем мы будем рассматривать только итерационные методы для решения задачи уточнения корня. Суть этих методов заключается в следующем.

По функции f(x) строится функция j(x) такая, что уравнениеx = j (x) равносильно уравнению  ( уравнения  f(x) = 0  и  x = j (x) имеют одинаковые корни). Затем рассматривается последовательность чисел  , где- начальное приближение корня. Последовательность {x_i} при выполнении некоторых условий сходится к корню x = c.

Процесс вычисления  называется итерационным процессом; последовательность называется последовательностью итераций.

Если последовательность {x_n} сходится к корню c, то, начиная с некоторого n, выполняется неравенство: |x_n – c| £ e. Вычисления на этом прекращается и x_n считается приближенным значением корня, вычисленным с точностью e.

Отметим, что e  – это погрешность численного метода, при этом не учитывается погрешность вычислений на ЭВМ. Последовательность  может сходиться, а может и не сходиться. Если последовательность  не сходится, то при реализации численного метода на ЭВМ получаем, как правило, машинное переполнение.

В дальнейшем будем рассматривать итерационные методы уточнения корня по следующей схеме:

1) условия на применение метода;

2) формула метода;

3) выбор начального приближения и сходимость метода;

4) условие остановки итерационного процесса.

2.4. Метод простой итерации

1. Пусть известен отрезок [a, b], который содержит один корень уравнения f(x) = 0. Функция f является непрерывно дифференцируемой функцией на этом отрезке (f(x)ÎC¹[a, b]). При выполнении этих условий можно применять метод простой итерации.

2. По функции f(x) строится функция j(x), удовлетворяющая трём условиям: она должна быть непрерывно дифференцируемой (j(x)ÎC¹[a, b]), такая, что уравнение x = j(x) равносильно уравнению f(x)=0; должна также переводить отрезок [a, b] в себя.

Будем говорить, что функция j(x) переводит отрезок [a, b] в себя, если для любого x Î[a, b],  y = j(x)  также принадлежит [a, b](y Î [a, b]).

На функцию j(x) накладывается третье условие:

.

Формула метода:   x_n+1 = j(x_n).

3. При выполнении этих трех условий для любого начального приближения x₀Î[a, b] последовательность итераций x_n+1 = j(x_n) сходится к корню уравнения:  x = j(x) на отрезке [a, b] ().

Как правило, в качестве x₀ выбирается один из концов [a, b].

4. Условие остановки итерационного процесса:

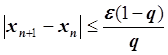, где e – заданная точность

Число x_n+1 при выполнении условия остановки итерационного процесса является приближенным значением корня уравнения f(x) = 0 на отрезке [a, b], найденным методом простой итерации с точностью e.

Пример

Построить алгоритм для уточнения корня уравнения: x³ + 5x – 1 = 0 на отрезке [0, 1] методом простой итерации с точностью e.

Решение

1. Функция f(x) = x³+5x-1является непрерывно дифференцируемой на отрезке [0,1], содержащем один корень уравнения.

2. Наибольшую трудность в методе простой итерации представляет построение функции j(x), удовлетворяющей всем условиям:

.

Рассмотрим: .

Уравнение x = j₁(x) эквивалентно уравнению f(x) = 0, но функция j₁(x) не является непрерывно дифференцируемой на отрезке [0, 1].