Вычислительная математика как часть математики, страница 9

φ₃(x) возрастает от   до , убывает от  до . Область изменения φ₃(x) полностью принадлежит ее области определения, следовательно, функция φ₃(x) переводит отрезок [1,2] в себя.

Выполнены все условия для функции φ(x), следовательно, .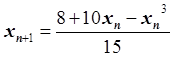

3. Начальное приближение: x₀ = 1.

4. Условие остановки итерационного процесса:

,                   .

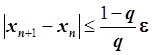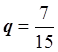Число x_n+1 , для которого выполняется условие остановки итерационного процесса, является приближенным значением корня уравнения, полученным методом простой итерации с точностью ε.

Задача 2

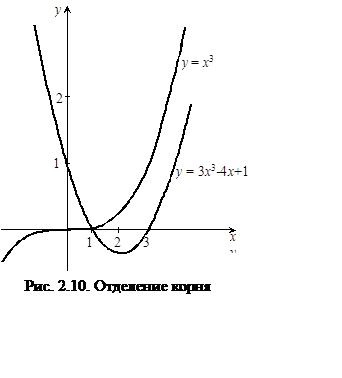
Отделить корни уравнения      x³ – 3x² + 4x – 1 = 0 и построить алгоритм для уточнения одного из них методом Ньютона с точностью ε.

Решение

Отделение корней

, отсюда .

Отрезок [0,1] содержит один корень уравнения (рис. 2.10).

Уточнение корня

Проверим условия для функции

,                       ,           .

Необходимо уменьшить отрезок [0,1] таким образом, чтобы уменьшенный отрезок содержал корень уравнения, и при этом выполнялись все условия для функции f(x).

Рассмотрим отрезок [0,0.9]:

,         , ,.

Отрезок [0,0.9] содержит один корень уравнения, и для него выполняются все условия для функции f(x). Функция f является дважды непрерывно дифференцируемой на этом отрезке, на концах отрезка принимает значения разных знаков, первая и вторая производные функции f не обращаются в ноль на этом отрезке.

2. Формула метода:.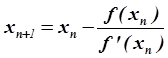

3. Начальное приближение:

, следовательно, .

4. Условие остановки итерационного процесса:

, где   .

При выполнении этого условия x_n+1 является приближенным значением корня уравнения, полученным методом Ньютона с точностью ε.

Задача 3

Отделить корни уравнения: 2^x  + 3x – 2 = 0 и построить алгоритм для уточнения одного из них методом хорд с точностью ε.

Решение

Отделение корней

, отсюда .

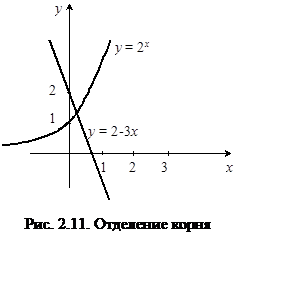
Отрезок [0,1] содержит один корень уравнения:   2^x + 3x – 2 = 0 (рис. 2.11).

Уточнение корня

1. Отрезок [0,1] содержит один корень уравнения, функция f является дважды непрерывно дифференцируемой на этом отрезке, на концах отрезка принимает значения разных знаков, первая и вторая производные функции f не обращаются в ноль на этом отрезке:

,   ,

, .

2. Формула метода:

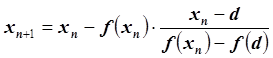, где d – неподвижная точка, , следовательно .

3. Так как d = 1, то начальное приближение x₀  = 0.

4. Условие остановки итерационного процесса:

,    .

При выполнении этого условия x_n+1 является приближенным значением  корня уравнения, полученным методом хорд с точностью ε.

Задача 4

Построить алгоритм  для вычисления  комбинированным методом хорд и касательных с точностью ε.

Решение

Отметим, что вычисление  с заданной точностью ε эквивалентно уточнению положительного корня следующего уравнения     x² – a = 0.

1. x² – 13 = 0. Положительный корень этого уравнения принадлежит отрезку [3,4]:

,             ,          .

,        на отрезке [3,4].

Функция f является дважды непрерывно дифференцируемой на этом отрезке, на концах отрезка принимает значения разных знаков, первая и вторая производные функции f не обращаются в ноль на этом отрезке.

2. , следовательно, слева применяем метод хорд, а справа – метод Ньютона. Формулы метода:

,

.

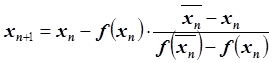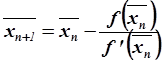3. Точки начального приближения: ,             .

4. Условие остановки итерационного процесса:

.

При выполнении этого условия 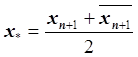 является приближенным значением , полученным комбинированным методом хорд и касательных с точностью ε.

Задача 5

Известно, что отрезок [1, 2] содержит один корень уравнения: . Построим алгоритм для уточнения этого корня методом итераций с точностью e.

Решение

1. Отрезок [1, 2] содержит один корень уравнения: .

Функция f является непрерывно дифференцируемой на этом отрезке (). Первая производная функции f не обращается в ноль на отрезке [1, 2].

 для x Î [1, 2].

2. Формула метода:.

 на отрезке [1, 2], следовательно, p > 0.

,              p = 8.

.

Проверим, что :

,

.

.

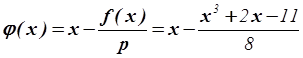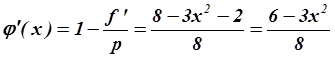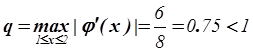3. Начальное приближение: .

4. Условие остановки итерационного процесса:

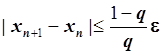,       q = 0.75.

Здесь , для которого выполняется условие остановки итерационного процесса, является приближенным значением корня уравнения, полученным методом итераций с точностью e.